Есть задача:
Дана полигональная сфера, где четко определена связь полигонов(общие вершины), сфера с одной стороны деформирована (вдавлена). Так же дан контур, спроецированный на поверхность деформированной сферы, как показано на рисунке, координаты его проекций на каждый полигон известны. И имеются 2 произвольные точки, например,

,

(показаны на рисунке). Требуется определить лежат ли эти точки внутри заданного контура.


Как я начал ее решать. Для определения находится ли точка внутри контура использовал классический алгоритм
Задача о принадлежности точки многоугольнику (учёт числа пересечений). Для этого соответственно производил переход из

в

пространство, т.е. сделал развертку исходной фигуры на плоскость. При этом положение каждого полигона в

определяется только правилами построения развертки и, в общем случае, не обязательно делать классическую развертку, а можно просто "разбить" сферу, т.е. считать, что каждый полигон находится в произвольном месте плоскости(единственное условие, что "нормали смотрят вверх", т.е. лицевые стороны полигонов смотрят на нас). Так на рисунке ниже приведена схема 2-х смежных полигонов, серой линией показаны связи по общим точкам, красной показано, что линия замкнутого контура переходит с одного полигона на другой. Сначала я строю отрезок из точки
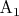
в произвольном направлении, получаем отрезок

в системе координат, построенной на базисе

. Определяю пересечение отрезка

с

. Далее надо оценить этот же отрезок относительно второго полигона (на рисунке "2") и его сегмента

. Просто оценить не выйдет, т.к. в текущей момент имеется разрыв контура на сегменты

и

.
Я делаю так:
- считаю, что базис первого полигона и второго построенные по смежной стороне

(

) одинаковы, а система координат имеет ноль в точке

(

), загвоздка только в том, что полигоны разбросаны на плоскости (но связи остались и мы можем найти смежные полигоны для данного);
- определяю координаты

в СК, построенной на базисе

(начинаю как и говорил с первого полигона)
- поскольку, считаю, что системы координат, построенные на базисах

и

"совпадают" (т.к. полигоны смежные изначально по

), т.е. можем полученные координаты отрезка

для СК на базисе

считать равными координатам в СК на

, а потом найдя матрицу перехода из из базиса

в

получить координаты

.
- далее просто оцениваем пересечения

и

- делаю аналогично для всех полигонов

Вопросы:
1. может есть другой способ решения подобной задачи (возможно, выше я написал , мягко говоря, не лучшее решение), буду благодарен за указание верного направления в решение подобной задачи
2. если взять спущенный футбольный мяч (с вмятиной как на представленной модели), сшитый из пентагонов (есть информация о связи смежных пентагонов), его разворачиваем в

, т.е. "расшиваем" где надо. Далее в

ставим точку внутри одного из пентагонов и из нее пускаем луч в произвольном направлении, когда луч пересекает границу исходного пентагона, он должен переходить в другой (как если бы мы пускали луч по поверхности сферы) и возвращаемся в исходную точку, естественно, он проходит и по "впуклости" мяча надо. Как используя

СК и информацию по связи смежных пентагонов построить такой луч, проходящий через множество пентагонов.



