Выловил глюк, теперь добавление четвёртой точки работает во всех случаях. Осталось доделать заполнение структур и проверить добавление ещё точек по одной. Однако мне не нравится как соединяются сайты:
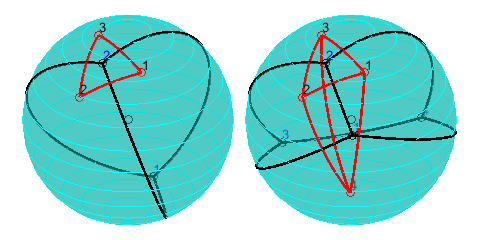
Это ни на что не влияет, но всё-таки хотелось бы придумать способ узнать, что сайты 3 и 4 надо соединить не по кратчайшему пути, а по наидлиннейшему. При этом не хотелось бы проверять наличие пересечения ребра 3-4 триангуляции со всеми остальными рёбрами. Вообще, во всех таких случаях
соответствующее ребро диаграммы лежит на другой стороне сферы. Как бы это утверждение математически формализовать?
-- 07.01.2018, 22:15 --Можно было бы воспользоваться проверкой расстояний. То есть считать, что точка C лежит вне отрезка AB, если
. Однако, если точка C лежит внутри отрезка AB, то по идее должно выполнятся равенство
, которое является единственной альтернативой предыдущему неравенству.
Перемудрил я с проверкой расстояний на плоскости. Если известно, что точки A, B и C лежат на одной прямой и необходимо определить, принадлежит ли точка C отрезку AB, то для этого надо проверить выполнение двух неравенств:
и
. Если оба неравенства выполняются, то точка лежит внутри отрезка, в противном случае — не лежит.
Кроме того, можно поступить чуток иначе, а именно проверить только первое неравенство
и проверить, что векторы
и
сонаправлены (например, что скалярное произведение больше нуля).
Первый подход на сферу (вернее даже на окружность), к сожалению, не переносим. Всё потому что между двумя точками на окружности есть два расстояния. Поэтому в ситуации на рисунке:
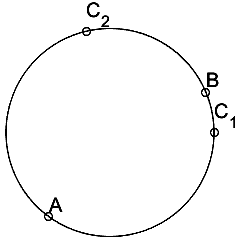
для обоих точек
выполняются неравенства
и
вне зависимости от того, принадлежность какой дуге AB — большей или меньшей — для точки С мы проверяем.
На сфере в этом плане вообще всё сложнее: для диаметрально противоположных точек A и B существует куча разных отрезков, принадлежность которым можно проверять. Впрочем, если задано, что точка C лежит на большой окружности (сферической прямой), проходящей через точки A и B, то вопрос только в том, как указать нужную половинку этой окружности.
Итак, возникла следующая задача. На сфере имеются три точки, например, A, B и C, лежащие на одной сферической прямой (большой окружности). Необходимо определить, лежит ли точка C внутри отрезка AB.
Решение надо начинать с правильного задания сферического отрезка. Я предлагаю его задавать специальной точкой —
центром сферической прямой (большой окружности). Для случая, когда две точки A и B не являются диаметрально противоположными этот центр прямой находится нормированием векторного произведения радиус-векторов точек A и B. Здесь подразумевается, что сфера единичного радиуса погружена в трёхмерное пространство и её центр совпадает с началом координат. Эта точка точка остаётся инвариантной при усечении, удлинении сферического отрезка, а так же при его переносе параллельно самому себе, если это так можно назвать. Своего рода направляющий радиус-вектор сферической прямой.
Следующей точкой, задающей сферический отрезок будет, естественно, его начало. С этим всё понятно. И последней задающей величиной является длина отрезка L. Она должна быть положительна и меньше
. Отрезок откладывается вдоль своей окружности против часовой стрелки, если наблюдать из центра окружности. Поэтому, например, справедливо следующее равенство:
![$\[\overrightarrow{{{R}_{B}}}=\overrightarrow{{{R}_{A}}}\cos L+\left[ \overrightarrow{{{R}_{A}}}\times \overrightarrow{{{R}_{cntr}}} \right]\sin L\]$](https://dxdy-02.korotkov.co.uk/f/d/8/6/d864d8b83981e44fe9fcea4fef58620d82.png "$\[\overrightarrow{{{R}_{B}}}=\overrightarrow{{{R}_{A}}}\cos L+\left[ \overrightarrow{{{R}_{A}}}\times \overrightarrow{{{R}_{cntr}}} \right]\sin L\]$")
. Такой подход весьма универсален, поскольку он позволяет однозначно задать любые сферические отрезки которые только можно себе вообразить, в том числе, длина которых больше кратчайшего расстояния между концами отрезка.
Теперь решение задачи о принадлежности. Последуем второму подходу, сделанному на плоскости. Проверим неравенство
, а так же проверим, что точка C откладывается в ту же сторону, что и точка B. Для этого вектор
![$\[\left[ \overrightarrow{{{R}_{A}}}\times \overrightarrow{{{R}_{C}}} \right]\]$](https://dxdy-02.korotkov.co.uk/f/1/0/1/10121afe5e1b53cca251a50749ecedb782.png "$\[\left[ \overrightarrow{{{R}_{A}}}\times \overrightarrow{{{R}_{C}}} \right]\]$")
должен быть сонаправлен с радиус-вектором центра окружности. Здесь, правда, есть тонкость, если мы допускаем возможность отрезков с длиной большей
. В этом случае, если
, то надо проверять
![$\[\left[ \overrightarrow{{{R}_{A}}}\times \overrightarrow{{{R}_{C}}} \right]\uparrow \uparrow \overrightarrow{{{R}_{cntr}}}\]$](https://dxdy-02.korotkov.co.uk/f/9/b/7/9b7f44f07ff98049af57fb464848a05f82.png "$\[\left[ \overrightarrow{{{R}_{A}}}\times \overrightarrow{{{R}_{C}}} \right]\uparrow \uparrow \overrightarrow{{{R}_{cntr}}}\]$")
, а если же
, то
![$\[\left[ \overrightarrow{{{R}_{A}}}\times \overrightarrow{{{R}_{C}}} \right]\uparrow \uparrow -\overrightarrow{{{R}_{cntr}}}\]$](https://dxdy-02.korotkov.co.uk/f/5/0/6/506633def7d104249be6433be5eb334582.png "$\[\left[ \overrightarrow{{{R}_{A}}}\times \overrightarrow{{{R}_{C}}} \right]\uparrow \uparrow -\overrightarrow{{{R}_{cntr}}}\]$")
. В случае
точки A и C диаметрально противоположны, и точка C лежит на любой окружности, проходящей через точку A. Это, правда, в теории. На практике погрешности округления в такой ситуации приведут к проблемам. Но в целом задача решена.
В моём случае, мне надо из двух диаметрально противоположных точек выбрать ту, которая принадлежит отрезку. Причём его длина не больше
, и гарантировано, что такая точка одна и только одна. Поэтому сравнивать расстояния не требуется, только сонаправленность векторного произведения и радиус-вектора центра окружности.
.
, в противном случае надо вывернуть ребро триангуляции на другую сторону сферы. Для большего числа точек ещё не пробовал, но для четырёх вроде всё время работает:
