УЗБЧ для арифметической функции количества

[vicvolf]

Рассмотрим арифметическую функцию количества натуральных чисел, обладающих определенным свойством - $Q(n)$.

Арифметическая функция $Q(n)$ является отображением: $Q(n): \mathbb {N }\to \mathbb {N}$.

$Q(n)$ является кусочно-постоянной, "ступенчатой", монотонно возрастающей функцией. Для нее выполняется:

$\lim_{n\to \infty} {Q(n)} = \infty$. (1)

Значение $Q(n)$ возрастает на 1, если натуральное $n$ удовлетворяет определенному свойству. В противном случае значение функции не изменяется.

Теперь докажем, что асимптотическая плотность $Q(n)$ равна:

$\lim_{n \to \infty} {Q(n)/n} = C$, (2)

где $C$- постоянная, $0 \leq C \leq 1$.

Так как $0<Q(n) \leq n$, то $0 < Q(n)/n \leq 1$. (3)

Учитывая, что $Q(n)/n$ монотонно убывающая функция и, на основании (3), ограниченная функция, то она имеет предел:

$\lim_{n \to \infty} {Q(n)/n} = C$.

В силу (3) значение $0 \leq C \leq 1$.

Естественно $\lim_{n \to \infty} {Q(n)/n} = 1$, если $Q(n)=n$.

Если $Q(n)=o(n)$, то $\lim_{n \to \infty} {Q(n)/n} = 0$,

Примерами $Q(n)$ являются арифметические функции: количество натуральных чисел, свободных от квадратов; количество простых чисел и.т.д.

Покажем, что усиленный закон больших чисел выполняется для $Q(n)$.

Для этого введем вероятностное пространство: $(\Omega,A,P)$, взяв $\Omega=\{1,2,\dotsc,n\}$, $A$ — все подмножества $\Omega$, $P(A)=\frac {|A|} {n}$, где $|A|$ - это количество членов натурального ряда, удовлетворяющих условию.

Таким образом, $P(A)=\frac {Q(n)} {n}$.

Образуем случайную величину $S_n=\sum_{i=1}^n {x_i}$, где $x_i=1$, если произошло событие $A$ (натуральное число удовлетворяет условию) и $x_i=0$, если нет.

Соответственно вероятности событий: $P(x_i=1)=p, P(x_i=0)=1-p$.

Следовательно, $Q(n)=S_n$ (4).

На основании усиленного закона больших чисел для испытаний Бернулли:

$S_n/n \to p$ (п.н.) при $n \to \infty$ (5).

Следовательно, на основании (2), (4), (5):

$Q(n)/n \to p$ (п.н.) при $n \to \infty$.


Все ли верно?

[Brukvalub]

Нет.

[ET]

vicvolf в сообщении #1278975 писал(а):

$\lim_{n\to \infty} {Q(n)} = \infty$. (1)

Почему? Ну ладно, пусть выполняется это... но тогда.

vicvolf в сообщении #1278975 писал(а):

Теперь докажем, что асимптотическая плотность $Q(n)$ равна:

$\lim_{n \to \infty} {Q(n)/n} = C$, (2)

Теперь уже не докажите. Например свойство :"четность числа цифр в десятичной записи".

vicvolf в сообщении #1278975 писал(а):

Учитывая, что $Q(n)/n$ монотонно убывающая функция

С чего бы вдруг? Как раз ничего подобного

[vicvolf]

ET Спасибо, но это не влияет на доказательство УСБЧ для $Q(n)$. Ссылку на (2) можно убрать. Здесь дело в другом. В доказательстве действительно имеется ошибка. Какая?

[--mS--]

Вам её уже указали:

ET в сообщении #1279089 писал(а):

vicvolf в сообщении #1278975 писал(а):

Учитывая, что $Q(n)/n$ монотонно убывающая функция

С чего бы вдруг? Как раз ничего подобного

[vicvolf]

--mS-- Предел отношения $\lim_{n \to \infty} {\frac {Q(n)} {n}}$ может существовать и быть в нужных пределах. Например, для арифметической функции количества натуральных чисел, свободных от квадратов: $\lim_{n \to \infty} {\frac {6n/\pi^2+O(n^{1/2})}{n}}=6/\pi^2$ или для количества простых чисел $\lim_{n \to \infty} {\frac {n/log(n)+o(n/log(n))} {n}}=0$. Но этого не достаточно, чтобы выполнялся УЗБЧ для $Q(n)$.
Все дело в том, что на конечном интервале натурального ряда $[1,n]$ отношение $\frac {Q(n)} {n}=P(A)$ является вероятностной мерой, а на бесконечном интервале натурального ряда $[1,\infty)$ предел $\lim_{n \to \infty} {\frac {Q(n)} {n}}$ не является вероятностной мерой, так как для него не выполняется аксиома счетной аддитивности.

[--mS--]

vicvolf в сообщении #1278975 писал(а):

На основании усиленного закона больших чисел для испытаний Бернулли:

$S_n/n \to p$ (п.н.) при $n \to \infty$ (5).

Не вижу, что тут обсуждать. Вы заводите величины в схеме серий, их количество меняется одновременно с ними самими. Какой УЗБЧ Вы применяете к этой схеме серий? Где сформулированы и проверены его условия?

[vicvolf]

--mS-- в сообщении #1279897 писал(а):

Какой УЗБЧ Вы применяете к этой схеме серий? Где сформулированы и проверены его условия?

Я использую Теорему Колмогорова о сумме независимых одинаково распределенных случайных величин с конечным математическим ожиданием. Точнее обращение этой теоремы на стр. 381 у Ширяева (Замечание 1) - Пусть $x_i$ независимые одинаково распределенные случайные величины и $S_n=\sum_{i=1}^n {x_i}$ и пусть с вероятностью равной 1 существует предел $\lim_{n \to \infty} {S_n/n} =C$, где $C$ - конечная константа. 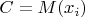Тогда $C=M(x_i)$ и $M(|x_i|)<\infty$. Для доказательства я использую:

RIP в сообщении #1256452 писал(а):

Любой начальный отрезок натурального ряда $\{1,2,\dotsc,n\}$ можно естественным образом превратить в вероятностное пространство $\left(\Omega_{n},\mathcal{A}_{n},\mathbb{P}_{n}\right)$, взяв $\Omega_{n}=\{1,2,\dotsc,n\}$, $\mathcal{A}_{n}$ — все подмножества $\Omega_{n}$, $\mathbb{P}_{n}(A)=\frac{|A|}{n}=Q(n)/n$. Тогда произвольную (вещественно- или даже комплекснозначную) функцию $f(k)$ натурального аргумента (а точнее, её ограничение на $\Omega_{n}$) можно рассматривать как случайную величину $S_{n}$ на этом вероятностном пространстве: $S_{n}(k)=f(k)$, $1\leqslant k\leqslant n$.

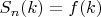
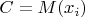
Следовательно, если при фиксированном $n$ в данном вероятностном пространстве случайную величину $S_n(k)=f(k)$ можно представить, как $S_n=\sum_{i=1}^n {x_i}$, где $x_i$ - независимые одинаково распределенные случайные величины, и $\lim_{n \to \infty} {S_n/n} =C$, где $C$ - конечная константа. Тогда $C=M(x_i)$ и $M(|x_i|)<\infty$.

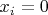
Арифметические функции количества натуральных чисел, удовлетворяющих определенному свойству - $Q(n)$ можно представить в виде $S_n=\sum_{i=1}^n {x_i}$, где $x_i=1$, если натуральное число $i$ удовлетворяет определенному свойству и $x_i=0$, если нет. Надо только в качестве $P(x_i=1)=p=Q(n)/n,P(x_i=0)=1-Q(n)/n$.

Осталось только для конкретной арифметической функции проверить выполнение условия: $\lim_{n \to \infty} {Q(n)/n} =C$. Например, как показано в последнем сообщении, это выполняется для арифметических функций $Q(n)$: количества натуральных чисел, свободных от квадратов, количества простых чисел и других. В этом случае выполняется УЗБЧ для арифметической функции $Q(n)$: $\lim_{n \to \infty} {Q(n)/n} =M(x_i)$, где $M(x_i)=p$, как для случайной величины Бернулли.

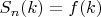
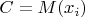
УЗБЧ можно обобщить на произвольную арифметическую функцию, для которой выполняются условия,т.е. при фиксированном $n$ в данном вероятностном пространстве случайную величину $S_n(k)=f(k)$ можно представить, как $S_n=\sum_{i=1}^n {x_i}$, где $x_i$ - независимые одинаково распределенные случайные величины, и $\lim_{n \to \infty} {S_n/n} =C$, где $C$ - конечная константа. Тогда $C=M(x_i)$ и $M(|x_i|)<\infty$. Например, указанные условия выполняются для функции Мертенса.

[--mS--]

Никакого отношения сформулированный УЗБЧ не имеет к данной схеме серий.

[vicvolf]

Это более общий случай, из которой УЗБЧ для схемы Бернулли и соответственно для арифметической функции количества вытекает, как частный.
С наступающим Новым годом!

[Brukvalub]

Для начала, заметим, что в формулировке УЗБЧ рассматриваются "независимые одинаково распределенные с.в." Где проверено требование независимости?

[vicvolf]

В данном вероятностном пространстве:

RIP в сообщении #1256452 писал(а):

Любой начальный отрезок натурального ряда $\{1,2,\dotsc,n\}$ можно естественным образом превратить в вероятностное пространство $\left(\Omega_{n},\mathcal{A}_{n},\mathbb{P}_{n}\right)$, взяв $\Omega_{n}=\{1,2,\dotsc,n\}$, $\mathcal{A}_{n}$ — все подмножества $\Omega_{n}$, $\mathbb{P}_{n}(A)=\frac{|A|}{n}=Q(n)/n$. Тогда произвольную (вещественно- или даже комплекснозначную) функцию $f(k)$ натурального аргумента (а точнее, её ограничение на $\Omega_{n}$) можно рассматривать как случайную величину $S_{n}$ на этом вероятностном пространстве: $S_{n}(k)=f(k)$, $1\leqslant k\leqslant n$.

при фиксированном $n$ все события равновероятны и независимы.

[Brukvalub]

vicvolf в сообщении #1280455 писал(а):

при фиксированном $n$ все события равновероятны и независимы.

Напрасно вы думаете, что слово "независимы" является мантрой, которую достаточно просто произнести, и все получится само собой.
Понятие "независимые с.в." имеет определение, и прежде чем использовать независимость с.в., ее нужно ОБОСНОВАТЬ, а не просто раз за разом голословно выписывать слова "эти с.в. независимы".

[--mS--]

По-моему, пора тему уносить в пургаторий.

[Brukvalub]

--mS-- в сообщении #1280491 писал(а):

По-моему, пора тему уносить в пургаторий.

Согласен. "Научные изыскания" ТС напоминают мне ответ студента-неуча на экзамене, пытавшегося хоть что-то выучить в ночь перед экзаменом. Такие же вырванные из контекста куски формулировок без какого-либо понимания их смысла и условий применимости, беспомощные ссылки на авторитетов типа "не знаю что и как, но ТАК БЫЛО НА ЛЕКЦИЯХ!!!!"