Это было доказано для любого

, верно?
Да.
Вот до этого места всё понятно?
Можно сказать понятно.
После этого останется сделать один маленький шаг.
Рассмотреть два случая для

и для

, для первого доказано существование нижней границы, для второго - верхней, которая станет нижней после перехода
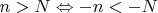
Сейчас мне кажется, что с доказательством я разобрался.
Если Вам уже известно, что

Не знаю известно или нет:
Если говорить в контексте школьных знаний, я бы сказал, что да. Если говорить в контексте Зорича, то с одной стороны как бы нет(определение "Пусть

. Для
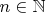
полагаем по индукции
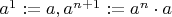
" дано на 138 странице, лемма дана на 71 странице) С другой стороны, раз нового, уточненного, определения нет, предполагается, что нужно пользоваться школьным "очевидным"(не в смысле "просто", а в смысле "основано на интуитивном понимании") определением(?), тогда ответ все-таки да. Сама лемма по школьному "очевидна". Раз ее доказывают, предполагается использование нового, уточненного подхода. Начинаю гадать пропустил я что-то или нет. На это уходит очень много времени. Если можно посоветовать что-то в этой ситуации - посоветуйте, пожалуйста.
Та же проблема с
Зорич, стр 72 писал(а):
Та же проблема с

(достаточно того, что это интуитивно "очевидно" или обоснование очень простое и мне нужно решать упражнения...) Вот неравенство треугольника по школьному "очевидно"

, но его ддоказывают, а не пишут, что исходя из определения модуля.
Похоже на то :)
Спасибо, что не смотря на это Вы мне ответили!



