Задана лагранжева система с лагранжианом

функция

гладкая на указанном множестве и

-периодическая по

, кроме того

и

.
Доказать, что система имеет решение

, периодическое в следующем смысле
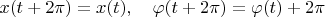
(Задача сформулирована специально в рафинированном виде для олимпиадного раздела, обобщения мне известны, спасибо.)