Это верно, не совсем верно или чушь?
Да!
1. Посмотрите, что получится для матриц два на два (расписав как систему четырех уравнений). Сравните с Вашим ответом.
2. Посмотрите для жордановой нормальной формы (напр., для диагональной А) (к этому всегда можно свести)
-- 19.12.2017, 02:53 --3. Такого сорта уравнения возникают при приведении линейной системы

заменой

к виду
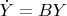
: получается
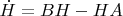
. Для

такую легко сочинить: достаточно решение

умножить (слева) на
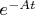
, затем на

, и на

....
-- 19.12.2017, 02:58 --А вааще, токого типа дифуры - из теории групп Ли: посмотрите про экспоненциальное отображение, действие слева-справа, и присоединенное действие