То есть почему, уже начиная с цифр

перестает выполняться равенство?

Расчет проводил в Wolfram matematik
Wolfram Mathematica 9.0. И правда кучу сообщений выдаёт, когда вычисляет сумму интегралов. И результат не совпадают с результатом вычисления интеграла в левой части. Видимо, вычисления оказались сильно неточными.
Но я поэкспериментировал с параметром WorkingPrecision. Наибольшее значение, с которым вычисление левой части прошло без лишних сообщений, оказалось
WorkingPrecision -> 33. Результат:

.
При вычислении суммы интегралов наименьшим возможным оказалось значение
WorkingPrecision -> 35. Результат:

.
И есть другие полезные параметры.
У Вас в процитированной формуле имеется лишний знак доллара после первого интеграла.
-- Ср дек 13, 2017 15:26:29 --Забыл сказать. Значение

я задавал в виде обыкновенной дроби
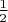
, а не в виде десятичной дроби

. Иначе появляются предупреждения о недостаточной точности задания подынтегральной функции.



