К сожалению в формулы перехода вкралась ошибочка!
Не порядок, ее надо исправить.



Старое решение:
Минимальные пифагоровы тойки:

,
где

- взаимно простые числа различной четности.
Новое решение:
Минимальные пифагоровы тойки:

,
где

- взаимно простые нечетные числа.[

;

,

,

.

,

,

;

;

,

,

.


.
-- 12.12.2017, 16:26 --Теорема Ферма гласит: нет таких натуральных чисел

,
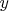
и

,
которые бы при целой степени

удовлетворяли уравнению

.
При

уравнение решений не имеет, а при

уравнение

имеет решения.
Уравнение

является частным случаем уравнения Ферма

при

,
поэтому она и называется теоремой Ферма при

.
Ну, не нравится Вам теорема Ферма, назовите ее теоремой Пифагора.



