Голосованием я ничего решать не согласен.
Разумеется. Никто и не предлагал. Вполне может быть прав один против многих. Но это не тот случай.
Вы считаете, что эти раздачи неразличимы?
Да. Потому что решать надо для
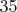
карт. А какая выбыла — в данной задаче не имеет значения.
Я вижу три простых для понимания способа решения задачи.
1. Найти количество исходов, благоприятствующих данному событию и разделить их на общее количество исходов

2. Тот, что предложил
fred1996. Перемножить

вероятностей для козырей.

3. Перемножить

вероятностей для не козырей.

В последнем случае, доставая по одной карте из колоды, мы умножаем вероятности того, что вытащенная карта не козырь. И находим вероятность того, что за

попыток мы так ни разу и не вытащим козырь.