(насчёт раздела)
Не знал, в какой раздел стоит писать, решил, что всё-таки в физический. Во-первых, происхождение задачи физическое. Во-вторых, физики к таким интегралам как-то более привычны, думаю. Наконец, в ПРР(М) меня, думаю, камнями закидают за столь вольное обращение с математикой.
Требуется вычислить интеграл типа

с

где

,

,

- некоторые константы, а

-
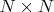
матрица единиц.
Поскольку интеграл гауссового типа, то ответ будет вида

, то есть нужно найти выражение для обратного оператора. Поскольку выражение для

содержит

, это имеет смысл делать в фурье-представлении. Получим :

где

и

Этот оператор может быть сравнительно просто обращён. Импульсная и "компонентная" части могут быть обращены независимо друг от друга (?), при этом

-часть диагональна, поэтому её обращение тривиально. Для "компонентной" же части
ответ такой:

с

,
и

Тогда в пределе

имеем что-то вроде

(с интегрированием по

).
Проблема в том, что

содержит

, из-за чего появляется слагаемое типа

. Да и в целом факт того, что появится слагаемое с 3 дельта-функциями и лишь 2 интегрированиями, меня напрягает. Где-то мог со знаками, коэффициентами и прочим накосячить, но принципиальный момент заключается в том, что из-за слагаемого

в начале в итоге получается какая-то чепуха. У меня была идея притвориться столбом и просто ввести

, чтобы формально избавиться от проблемы, но по многим причинам делать мне этого не хочется.
В общем, как аккуратно разобраться с интегралом?



