Аксиома бесконечности как раз постулирует существование хотя бы одного индуктивного множества

, и коль скоро мы уже определили предикат «

— индуктивное», мы сможем написать «

— элемент каждого индуктивного множества» и выделить им из

интересующее пересечение.
У меня почти получилось, но не до конца:
План:
1 построить минимальное по включению множество, выделив из некоторого индуктивного множества подмножество, все элементы которого принадлежат всем индуктивным множествам
2 показать, что полученное множество - индуктивное
3 показать, что полученное множество совпадает с пересечением всех индуктивных множеств
1 Согласно аксиоме бесконечности существует некоторое индуктивное множество

. Если свойство индуктивности обозначить

, то используя аксиому выделения можно построить множество
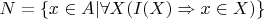
2 Исходя из того, как построено


. По определению пустое множество принадлежит любому индуктивному множеству, откуда

Пусть

, тогда
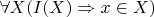
По определению индуктивного множества

Поскольку истинность
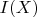
делает истинным

,

можно заменить на
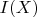
, тогда

Поскольку

индуктивное

, тогда воспользовавшись

, получается что

Значит

- индуктивное множество.
3 По определению

Поскольку

- индуктивное, каждый элемент пересечения всех индуктивных множеств

принадлежит

. Если обозначить множество всех индуктивных множеств

, то
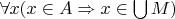
. Подставив это в

получается

, учитывая что

получается что

Согласно аксиоме объемности

Проблема, которая осталась - это то как построить множество всех индуктивных множеств, чтобы пересечение и объединение всех индуктивных множеств были определены. Можно применять аксиому пары, к полученной паре применять аксиому объединения, из результата и некоторого индуктивного множества опять строить пару и снова применять аксиому объединения и так далее. Но так получится построить только объединение любого количества индуктивных множеств, а не всех. Если бы получилось построить объединение всех индуктивных множеств, то к нему можно было бы применить аксиому множества подмножеств и из результата по аксиоме выделения выбрать все индуктивные подмножества, получив множество индуктивных множеств.



