Здравствуйте, у меня есть две проблемы, прошу помощи в том что бы их разрешить.
1) Есть поверхностный интеграл 2 рода:

, где S - верхняя сторона поверхности

и

Я рассуждал так, можно воспользоваться свойством аддитивности и разделить исходный интеграл на сумму трех интегралов. И по скольку

входят в этот интеграл симметрично, достаточно посчитать любой один из них и результат умножить на три. Я решил брать

. Т.к.

, получаем

. Перейдем в полярные координаты и получим:

. Тогда в конечном итоге получаем ответ:

.
Я не до конца уверен в правильности своих действий в начале решения. Скажите, пожалуйста, справедливы ли они?
2) Вторая проблема заключается в том, что я не могу разобраться с пределами интегрирования в тройном интеграле:

, где V:

Мои рассуждения: по всей видимости, необходимо рассматривать два случая: когда верхней границей является сфера

, а нижней фигура

, а второй случай: верхняя граница - фигура

, нижняя - сфера

. Далее, из каждого уравнения выразил z:

и
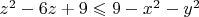
т.е.

или

. А как развивать дальше, что делать с пределами интегрирования никак не могу сообразить.
Направьте или помогите оттолкнуться, пожалуйста.



