Здравствуйте. Есть следующая задача:
Если есть норма на линейном пространстве, следует ли из этого, что существует метрика. И наоборот
И так. Пусть задано линейное нормированное пространство K. Тогда мы можем определить метрику, как норму разности двух элементов из пространства K
(

по свойству линейного пространства

то

)
Проверим, является ли такая функция метрикой:
1)

;

по определению нормы
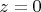
тогда и только тогда, когда

2)
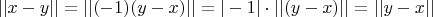
- является симметричный отношением
3)
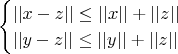
сложим неравенства

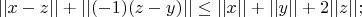




Так же выполняется неравенство треугольника
Поскольку, восполняются все аксиомы метрики, тогда

является метрикой. Это означает то, что если на линейном пространстве задана норма, то существует метрика.
A вот как доказать или опровергнуть обратное. что-то в голову не приходит. И правильно я, вообще, выполнил доказательство существования метрики на линейном нормированном пространстве?