Вероятность - это не промежуток, это число.
Вероятность - это число, да. Про
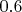
я думаю как про

, а про

как про наступление примерно в

случаях из

. "Примерно" в смысле что число наступлений события будет стремится к

при увеличении числа экспериментов. Тут всё правильно?
вероятность попасть точно в точку
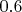
равна нулю
Она нулевая, потому что отрезок
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
содержит бесконечное число точек, да? Но несмотря на нулевую вероятность выпасть может. Потому что вероятность любого наперед заданного числа будет нулевая, из-за того что чисел бесконечно в интервале действительной прямой. Так?
Нет, так никто не делает и это в общем случае бессмысленно.
Если нужно в компьютерной программе работать с вероятностями, то как поступают? Вот два несовместных события

,

. Я думал что так: возьмём генератор случайных чисел, сгенерируем число из
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
, если выпавшее число принадлежит
![$[0,0.6]$ $[0,0.6]$](https://dxdy-02.korotkov.co.uk/f/1/9/0/190b490348cd82c6a6bbbbb9630ab1bc82.png)
то событие

, а если нет то

. Так никто не делает?



