1) Сумма и произведение измеримых функций --- измеримые функции.
2) При
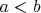
функции

и

измеримы.
3) Каждая непрерывная функция измерима.
4) Любую функцию с конечным числом точек разрыва можно получить из непрерывной функции и функций, описанных в пункте 2, при помощи сложений и умножений.
Добавлено спустя 7 минут 23 секунды:
Тьфу, блин, это верно только для функций, имеющих конечные пределы слева и справа в любой точке. Но всё равно задача простая
 Добавлено спустя 13 минут 36 секунд:
Добавлено спустя 13 минут 36 секунд:
Надо так.
1) Сумма измеримых функций --- измеримая функция.
2) Для непрерывной функции

функция

измерима (здесь

).
3) Функция

измерима при всех

.



