Для начала повторю п. 6 в начале странице для удобства обсуждения и копирования - с исправленными опечатками
6. Для тех, кто решил читать заметку с этого пункта, дадим сводную информацию. Язык

из класса

соответствует следующему алгоритму проверки (по которому язык

и можно отнести к классу

) –

. В неисключительных случаях (об исключительных будет в п. 6.1) аргументы «не подтвердят» слово языка и результат будет

(Ноль), если не будет исполнено хоть одно из следующих условий:

– число, записанное в позиционном виде (например, в десятичном – вроде 3001) :

, где алгоритм

возвращает строку длиной

, состоящую только из символов «1»;

– текст (программный код) некоторого алгоритма типа

или же текст

;

– текст некоторого утверждения на языке теории Пеано;

– текст некоторого доказательства на языке теории Пеано;

– размер текста y ограничен:

, где

,

– некоторая фиксированная степень, и, разумеется, условие на размер нарушено, если

;
Утверждение с текстом в

доказывается доказательством с текстом в

в рамках теории Пеано (или любой другой заранее оговорённой теории арифметики, если она более полная и удобная для наших целей, чем теория Пеано);
Если случай не из пункта 6.1 и перечисленные условия выполнены, то:

.
Ещё мы условились, что записи вида

или

обозначают текст утверждения

на заранее оговоренном языке логики и программный код (тоже текст, фактически) алгоритма

, записанный оговорённым способом представления алгоритмов в выбранной за основу языка

теории первого порядка (теория Пеано способна представлять алгоритмы, но не очень наглядно – тут есть что улучшать для практических нужд).
И, разумеется, мы пользуемся не «гёделевыми номерами», которые дают неполиномиально огромное представление для информации (число 10, например, имеет вид «1111111111»), а принятым в «человеческом» и «компьютерном» мире представлением в виде текстов и чисел в позиционном (десятичном, например) представлении.
Теперь – о времени работы алгоритма проверки для разных случаев, словах языка

, сертификатах, их размере и исключениях:
6.1. Для случаев, подходящих под шаблон

количество шагов работы – в пределах полинома

. В силу того, что в данном случае

, чей размер полиномиально зависит от размера

и от размера

, а при этом

, то в

можно заменить

на

и ограничивающий алгоритм останется ограничивающим (количество шагов работы алгоритма проверки не превысит результат данного ограничивающего алгоритма) и при этом он останется полиномиальным. И его тогда можно переписать в виде:

(что равно

).
Проверку под шаблон 6.1 алгоритм

проводит в первую очередь и – если соответствие обнаружено – возвращает

в пределах указанного времени (количества шагов).
Кстати, многоточия в конце

стоят потому, что аргументы

в данном случае не используются и тут алгоритм зависит, фактически, от трёх аргументов, возвращая

:

.
И, напомню, случай 6.1 относится к тому слову (словам!), принадлежность которого отвергается и смысл этого отказа такой: «Алгоритм

не может найти доказательство для утверждения

». Можно было бы добавить «…в пределах доказательств допустимого размера», но найти доказательство для утверждения

алгоритм

не может в принципе. Поэтому не может «вообще» и, в силу этого, «…в пределах доказательств допустимого размера» в том числе. Подробнее:
Алгоритм-решение

решает вопрос о принадлежности языку

слова вида 1:

; с сертификатом вида 1:

.
При этом сам алгоритм-решение в этом решении соответствует части сертификата

и из пункта 6.1 за количество шагов в пределах

можно узнать от алгоритма проверки

, что никакого подтверждающего сертификата с такой частью

для данного слова найти невозможно – что соответствует тому факту, что алгоритм

не может корректно подтвердить (выдать в качестве результата

) слово

(оно построено в соответствии с теоремой о неопределимости для данного алгоритма-решения).
При этом в языке

помимо слов вида 1, есть и
слова вида 2:

; с сертификатом вида 2:

.
И данный ответ алгоритма проверки из пункта 6.1:

соответствует отсутствию в языке

слов вида 2:

; с сертификатами вида 2:

.
То есть, хоть алгоритм-решение

должен решать вопрос о принадлежности языку

слов вида 1, но при

он даёт правильный ответ с точки зрения непринадлежности языку

слова вида 2:

. Но непринадлежность языку данного слова вида 2 соответствует как раз невозможности найти подтверждающий сертификат с частью

для слова вида 1:

.
В случае 6.1 ограничивающий алгоритм

не зависит от

,

. Но от них не зависит и работа

в случае, подходящем под шаблон пункта 6.1.
6.2. Для остальных случаев количество шагов работы алгоритма проверки – в пределах

, впрочем, и пункт 6.1 соответствует пункту 6. Но случай 6.1 является более жёстким ограничением – неполиномиально более жёстким, так как в случае 6.2 членом полинома является размер
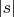
, растущий экспоненциально относительно размера

.
Случай 6.2. в равной степени относится к словам вида 1 и 2, не попадающими под шаблон пункта 6.1:
слова вида 1:

; с сертификатом вида 2:

.
слова вида 2:

; с сертификатом вида 2:

.
Для слов вида 1 суммарный размер сертификата ограничен (требование корректности) алгоритмом

, где

– некоторая фиксированная степень:

, что повторяет сказанное в начале пункта 6 про размер доказательства

:

,
а последнее ограничение соответствует сертификату вида 2. Для обоих вариантов, как видим, ограничение сертификата является полиномиальным относительно размера слова.
И кроме специальных случаев из 6.1 – при котором соответствующие слова языку

как раз не принадлежат – в остальном принадлежность слов вида 1 и вида 2 языку

(при корректных

) ничем не отличаются друг от друга. Такая «одинаковость» (кроме спец. случая) связана с тем, что в языке

мы учитываем только ту ограниченность возможностей алгоритмов-решений, которая следует из теоремы о неопределимости. Но эта ограниченность полностью исчерпывается специфическими случаями (хоть их и бесконечное количество для каждого алгоритма-решения) из пункта 6.1.
6.3. Если алгоритм-решение

для слова из специального случая 6.1 возвращает

при корректном

:

(случай 1),
то доказательства для утверждения

нет, и, напротив, имеется доказательство для его отрицания. То есть, ответ данного алгоритма-решения на данном слове в этом случае заведомо не корректен.
Если же алгоритм-решение

для слова из специального случая 6.1 возвращает

при корректном

:

(случай 2),
то логическое доказательства для утверждения

имеется, но, вопрос – соответствует ли размер данного доказательства допустимым размерам:

.
Но если размер данного доказательства соответствует указанному пределу, то ответ данного алгоритма-решения на данном слове и в этом случае оказывается не корректным.
Если же алгоритм-решение

для слова из специального случая 6.1 не возвращает никакого ответа при корректном

(случай 3), то данное слово действительно не принадлежит языку

и это подтверждается при любых сертификатах алгоритмом проверки. То есть, и в данном случае работа алгоритма-решения

оказывается не корректной.
Значит, единственный случай, при котором алгоритм-решение

может выдать корректный результат – случай 2. И результат этот должен быть

. И этот результат соответствует результату работы алгоритма проверки

за полиномиальное количество шагов работы – в пределах

(что равно

).
Поэтому при сведении нашей задачи из класса

в класс

полиномиальность времени проверки для случая 2

должна превратиться в полиномиальность времени на обнаружение решения (или невозможности решения) вида

.
И вот идея доказательства для

:
Здесь очевидно, что при достаточно больших

данное предельное время работы алгоритма-решения из случая 2 экспоненциально мало по сравнению с допустимым размером доказательств:

, так как размер

экспоненциально велик по сравнению и с размером

, и с аргументами в

при достаточно больших

.
А это значит, что для достаточно больших

среди допустимых доказательств найдётся и то, в котором будет вывод и для случая 2:

, и для вытекающего из него утверждения

. А это и будет означать, что алгоритм

не смог подтвердить истинность утверждения

для которого есть доказательство среди доказательств допустимого размера.
А поскольку алгоритм

произвольный, то это будет означать отсутствие корректных алгоритмов-решений, делающих язык

языком класса

. То есть – оказывается доказанным неравенство

.
Конечно, в нескольких абзацах выше изложено доказательство

в общих чертах, а детали – как строить вывод для утверждения

при корректном времени работы алгоритма-решения

и почему размер вывода будет допустимого размера – изложены в следующем разделе.
-- 02.10.2017, 16:04 --А теперь - на вопросы:
утверждение с текстом в

" имело бы смысл, если бы

было множеством текстов
Там речь об аргументе алгоритма проверки. У аргумента есть значение и это значение - текст. А когда речь о слове - то

обозначает ту его часть, которая тоже содержит текст утверждения. Но раз слово языка, то это должно быть истинное в теории Пеано утверждение.
Или там вообще произвольный алгоритм?
Да, произвольный. Или

. Разумеется, для

нет никакого

и при

\overline{-}$ условия п. 6.1 никогда не выполнены.
Верно ли, что этим языком является язык, состоящий из троек

и четверок

, удовлетворяющих
(условиям)
dmitgu в сообщении #1252198
писал(а):

– число, записанное в позиционном виде (например, в десятичном – вроде 3001) :

, где алгоритм

возвращает строку длиной

, состоящую только из символов «1»;

– текст (программный код) некоторого алгоритма типа

или же текст

;

– текст некоторого утверждения на языке теории Пеано;

– текст некоторого доказательства на языке теории Пеано;

– размер текста y ограничен:

, где

,

– некоторая фиксированная степень, и, разумеется, условие на размер нарушено, если

;
Вы упустили вот это:
Утверждение с текстом в

доказывается доказательством с текстом в

в рамках теории Пеано (или любой другой заранее оговорённой теории арифметики, если она более полная и удобная для наших целей, чем теория Пеано);
И упустили п.6.1 - некоторые слова не "проходят" из-за него.
Верно ли, что вы хотите явно построить язык, который принадлежит

, но не

?
Наоборот, конечно. Вы, наверно, опечатались. Если да - тогда дальше, но я сейчас на работе и может позже )



