Исполняю
обещание, данное неделю назад. Писанина заняла гораздо больше времени, чем ожидал (впрочем, это всегда так бывает, когда что-нибудь обещаю написать).
1. Предполагаем, что натуральный ряд

снабжён
дискретной топологией, то есть, каждое его подмножество является открыто-замкнутым.
Про фильтры и ультрафильтры все квалифицированные участники знают, но напишу минимальные сведения для тех, кто не знает. Также я буду иметь в виду натуральный ряд, хотя многое в том или ином виде верно и для любого бесконечного множества. Часть необходимых определений сформулирована
выше.
2. Семейство

подмножеств натурального ряда называется
ультрафильтром, если выполняются следующие условия:
1)

;
2) если

и

, то

;
3) если

и

, то

;
4) для любого

либо

, либо

.
Разумеется, это определение не является специфическим именно для множества натуральных чисел, точно так же ультрафильтры определяются для любого множества. Пункт 3) в этом определении является лишним, так как следует из 1), 2) и 4), и приведён здесь только потому, что условия 1), 2) и 3) дают определение
фильтра.
3. Ультрафильтр

называется
тривиальным, если

, и
свободным, если

(имеется в виду пересечение всех множеств, принадлежащих

).
4. Имеют место следующие утверждения.
1) Фильтр и, в частности, ультрафильтр является центрированным семейством множеств.
2) Ультрафильтр — это максимальный фильтр, то есть, если

— ультрафильтр, а

— такой фильтр, что

, то

.
3) Для каждого фильтра существует содержащий его ультрафильтр.
4) Если ультрафильтр

тривиален, то существует такой элемент

, что

; при этом

.
5) Если фильтр

содержит конечное множество, то все содержащие его ультрафильтры тривиальны, причём, их число не превосходит мощности этого множества.
6) Свободный ультрафильтр является сильно центрированным семейством.
7) Если

— свободный ультрафильтр,

,

, и симметрическая разность

конечна, то

.
5. Множество всех ультрафильтров в множестве подмножеств натурального ряда

обозначается

.
Для элемента

обозначим

. Это — некоторый тривиальный ультрафильтр.
Это позволяет определить инъективное отображение

по формуле
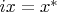
.
6. Топология на множестве

определяется следующим образом.
Для произвольного множества

определим множество

.
В качестве базы топологии на множестве

берётся семейство

.
Множество

, снабжённое такой топологией, является хаусдорфовым бикомпактным пространством, а отображение

—
вложением натурального ряда на всюду плотное подмножество пространства

(то есть, гомеоморфизмом на подпространство

). Это означает, что пара

—
хаусдорфово бикомпактное расширение натурального ряда. Заметим также, что на неформальном уровне обычно

и

отождествляются, а отображение

вообще не упоминается (это относится не только к данному случаю, но и вообще к расширениям топологических пространств).
Это расширение называется
расширением Стоуна—Чеха и является
максимальным в следующем смысле: если

— любое хаусдорфово бикомпактное расширение натурального ряда, то существует, и притом единственное, непрерывное отображение

, удовлетворяющее условию

для всех

. Последнее условие можно изобразить коммутативной диаграммой.
![$$\xymatrix{&&{\beta\mathbb N}\ar[dd]^{\varphi}\\ {\mathbb N}\ar[urr]^i\ar[drr]_j\\ &&{v\mathbb N}}$$ $$\xymatrix{&&{\beta\mathbb N}\ar[dd]^{\varphi}\\ {\mathbb N}\ar[urr]^i\ar[drr]_j\\ &&{v\mathbb N}}$$](https://dxdy-03.korotkov.co.uk/f/6/a/d/6ad3fc5bc8d20f9db6e1745996080b3e82.png) 7.
7. Свойства "операции"

:
1)

,

;
2)

;
3)

;
4)

;
5)

тогда и только тогда, когда

конечно;
6) множество

открыто-замкнуто в

для любого

.
8. Для произвольного подмножества

положим

, то есть,

— множество свободных ультрафильтров, содержащих множество

.
Можно также представить это множество как

.
9. Из свойства
7.6) следует, что для каждого элемента

множество

открыто в

. Поэтому для любого

множество

открыто, а множество

замкнуто в

, так как по свойству
7.6) множество

не только открыто, но и замкнуто в

.
В частности,

открыто, а

замкнуто в

. Топологическое пространство

называется стоун-чеховским
наростом натурального ряда. (В случае произвольного расширения

топологического пространства
 наростом
наростом называется

.)
Так как множества

,

, открыто-замкнуты в

и образуют в нём базу, то множества

также открыто-замкнуты в

и образуют в нём базу.
10. Свойства операции

1) множество

открыто-замкнуто в

;
2)
![$A^*=[iA]_{\beta\mathbb N}\setminus iA$ $A^*=[iA]_{\beta\mathbb N}\setminus iA$](https://dxdy-03.korotkov.co.uk/f/e/c/6/ec6228455ebce63ee04ac12bc7e75ee682.png)
(квадратные скобки обозначают замыкание в топологическом пространстве, указанном в индексе);
3)

тогда и только тогда, когда

конечно;
4)

тогда и только тогда, когда симметрическая разность

конечна;
5)

тогда и только тогда, когда

и

почти дизъюнктны;
6)

тогда и только тогда, когда

;
7)

тогда и только тогда, когда

;
8) если

— любое открыто-замкнутое множество, то существует такое множество

, что

.
11. 1) Семейство

подмножеств натурального ряда является сильно центрированным тогда и только тогда, когда семейство

является центрированным.
2) Семейство

бесконечных подмножеств натурального ряда является цепью тогда и только тогда, когда семейство

вполне упорядочено отношением

.
12. 1) Если

— счётное сильно центрированное семейство подмножеств натурального ряда, то это семейство имеет бесконечное псевдопересечение, то есть, существует такое бесконечное подмножество

, что

для всех

, поэтому семейство

также является сильно центрированным.
2) Более того, можно считать, что

для всех

, и если

— цепь, то

— тоже цепь, причём, построенное множество

является её наибольшим (в смысле

) элементом.
13. В терминах пространства

утверждения пункта
12 выглядят так:
1) если

— счётное центрированное семейство открыто-замкнутых подмножеств пространства

, то

содержит непустое открыто-замкнутое подмножество;
2) если

— счётное центрированное семейство открыто-замкнутых подмножеств пространства

, вполне упорядоченное отношением обратного включения

, то

содержит непустое открыто-замкнутое подмножество.
14. Кардиналы

и

в терминах пространства

могут быть определены так:
1)

— наименьшая мощность центрированного семейства открыто-замкнутых подмножеств пространства

с нигде не плотным пересечением;
2)

— наименьшая мощность семейства открыто-замкнутых подмножеств пространства

, вполне упорядоченного отношением обратного включения

, с нигде не плотным пересечением.



