(Оффтоп)
Предисловие.
Всем привет. Вчера запостил на
пикабу, местный аналог редита, доказательство для теоремы ферма. Поэтому тут будет копипаста от туда (вроде это не является рекламой). Сам я ошибки в доказательстве не нашел. Там её вроде тоже не нашли. Мне посоветовали обратиться суда.
Заранее извиняюсь за то что пост получился таким длинным и трудночитаемым.
 ; для того чтобы все решения для
; для того чтобы все решения для  ((A, B, C)- решения) были натуральными, они должны быть пифагоровыми тройками.
((A, B, C)- решения) были натуральными, они должны быть пифагоровыми тройками.
Краткая суть:
Имеем способ нахождения всех натуральных троек (их всего 3, возьмем тот, который алгебраический). Они (тройки) имеют вид

;

;

. Мы нашли все натуральные тройки! Все они удовлетворяют уравнению

!
Теперь по условию ищем все натуральные тройки удовлетворяющие

. Для

или 4, или 5, не важно, кароче для

.
Так как мы уже нашли все натуральные тройки, любое

должно удовлетворять

. А это возможно только в нулях.
Всё. Теорема решена.Теперь чуть подробнее:
(Оффтоп)
Всё началось с лекции Савватеева о дифантовых уравнениях:
https://youtu.be/RmyqOjF0yb8Нас интересует алгебраический способ решения - начинается на 39:48 и заканчивается на 56:06.
Итак, что мы имеем: мы нашли все рациональные точки на единичной окружности, то есть мы нашли все пифагоровы тройки (a, b, c рациональны и натуральны).
То есть, если a или b или c не натуральна/рациональна то она не является пифагоровой тройкой.
Пифагоровы тройки это частный пример теоремы ферма. Которая утверждает, что для

нету решений в натуральных целых числах отличных от ноля для

.
Рассмотрим графики

, где

для разных n:
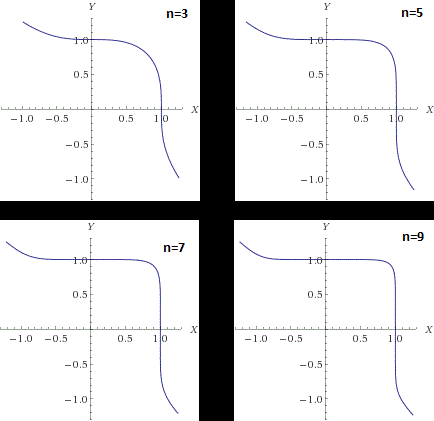
Вполне очевидно что при росте n график все дальше уходит от окружности, которой он является при

.
А теперь само решение:
!!! Ключевое утверждение - для  ; для того чтобы все решения для
; для того чтобы все решения для  ((A, B, C)- решения) были натуральными, они должны быть пифагоровыми тройками.
((A, B, C)- решения) были натуральными, они должны быть пифагоровыми тройками.
Доказательство ключевого утверждения
1) преобразуем

в

(Такие что

;

)
2) построим график для любого нечетного

(по правилам форума

)
3) на этом графике возьмем любую точку (точку S) и проведем из неё перпендикуляр на оси абсцисс и ординат.
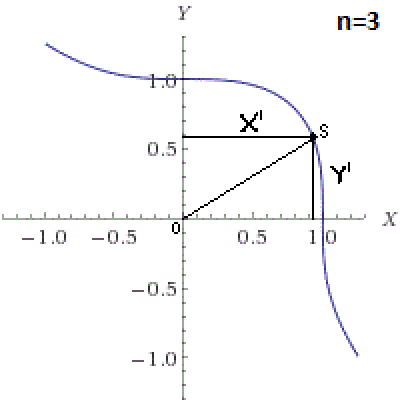
4)мы получим вертикальную длинну(скажем Y'), горизонтальную(скажем X') и длинну от нуля до самой точки(скажем OS).
5)то есть мы получили треугольник в рациональных числах.
6)Что бы (Y'; X'; OS) были рациональны они должны быть в числе пифагоровых троек (все которые мы нашли ранее удовлетворяют

).
Грубо говоря Любое решение

входит в множество решений

.
Теперь решаем простую систему уравнений:

Самое простое решение - решение построением.
Опять делаем преобразование и строим окружность

;
и график

.
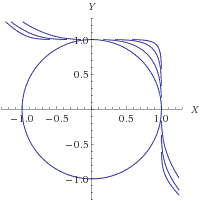
График при

Наглядно видно что для любого n > 2 эти два графика пересекаются исключительно в нулях (

либо

). А больше решений нет.



