Улетаю в отпуск, и хочу перед отъездом выложить все что накопилось нового.
Но сначала соберу в одном месте ваши старые вопросы/замечания, с которыми я пока не разобрался. Это для своего удобства, чтобы не забыть вернуться к ним потом.
(Долги)
1) Задача 11.
А ещё лучше в данном случае -- дать простой (насколько сможете -- чем проще, тем лучше) пример счётного набора замкнутых множеств с отсутствующей предельной точкой в объединении.
Контрпример: множество

всех рациональных чисел
...
это самый простой пример который я смог придумать.
Ещё гораздо проще есть.
2) Задача 14.
у Вас в той задаче нет целостного рассуждения -- от условия задачи, через определения и теоремы / другие задачи, к выводу. У Вас там интуитивное рассуждение, которое не выглядит убедительным.
Пути, как это исправить, Вам предложили -- и ewert и я (лучше всё же идти по пути ewert -- он короче и естественней).
Проще не ссылаться на ту задачу, а повторить ключевую часть её доказательства. Берём любую точку открытого множества и строим для неё максимальный интервал. Что можно сказать про его концы?...
3)
И, пожалуйста, поищите простой контрпример к Вашему утверждению: счётное объединение непересекающихся отрезков замкнуто.
4)
Поскольку в 14-й важна полнота

(попытайтесь угадать, почему), а в 15-й -- нет.
А вот новое.
Задача 16.
Пусть множество

открыто, множество

замкнуто. Можно ли утверждать, что множества

открыты или замкнуты?
Ответ.
Про

ничего утверждать нельзя. Например, пусть
![$A=(0,2),B=[1,3]$ $A=(0,2),B=[1,3]$](https://dxdy-02.korotkov.co.uk/f/9/d/b/9db06c7e618e3ea66dd95938489f3e2782.png)
. Тогда

-- не открыто (точка

не является внутренней) и не замкнуто (не содержит предельную точку

).
Про
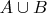
ничего утверждать нельзя. Пусть

не пересекаются, например
![$A=(0,1),B=[1,2]$ $A=(0,1),B=[1,2]$](https://dxdy-02.korotkov.co.uk/f/d/5/8/d584bbdcb587411bda043e0eec3dd56382.png)
. Тогда
![$A\cup B=(0,2]$ $A\cup B=(0,2]$](https://dxdy-03.korotkov.co.uk/f/a/7/e/a7eecadda29e8808be15ff5b3239629a82.png)
-- не открыто и не замкнуто.

открыто.
Доказательство.
Используем формулу

(а откуда ты взял эту формулу?)
Это задача 10.д листка 1, который я перепрыгнул. Сейчас у меня не получилось с наскока доказать ее, и есть сомнения что она в принципе верна. В своих попытках я пробовал использовать формулу

(задача 10.б листка 1), которая очевидно верна. Получил формулу
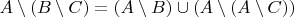
, с которой пока не придумал что делать дальше.
для выражения дополнения:

Множество

замкнуто (задача 15). Объединение двух замкнутых множеств замкнуто (задача 9). Из замкнутости дополнения следует открытость исходного множества (задача 15).

замкнуто.
Доказательство аналогично предыдущему пункту. Найдем дополнение:

Множество

открыто (задача 15). Объединение двух открытых множеств открыто (задача 2). Из открытости дополнения следует замкнутость исходного множества (задача 15).
-- 25.08.2017, 12:01 --Определение 7.
Множество

называется замыканием множества

.
Задача 17.
Если

замкнуто, то

.
Доказательство.
Следует из определения замкнутости:

.
-- 25.08.2017, 12:02 --Задача 18.
Замыкание любого множества замкнуто.
Доказательство.
Из задачи 17 следует, что замыкание замкнутого множества замкнуто.
Рассмотрим теперь незамкнутые множества. Пусть

-- незамкнутое множество,

-- предельная точка множества

, и пусть
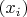
-- сходящаяся к

последовательность точек множества

. Все члены
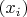
принадлежат

или

. Значит,
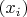
содержит сходящуюся к

подпоследовательность (задача 10 листка 11), целиком состоящую из точек множества

или целиком состоящую из точек множества

. Т.е.

является предельной точкой множества

или предельной точкой множества

. Отсюда вследствие замкнутости

следует, что

, и значит

.
-- 25.08.2017, 12:03 --Задача 19.
Замыкание множества

есть пересечение всех замкнутых множеств, содержащих

.
Доказательство.
Пересечение всех замкнутых множеств, содержащих

, содержит

. Каждое множество из пересечения содержит также

(вследствие своей замкнутости). Следовательно, пересечение содержит

. Включение

и

в пересечение означает включение

в пересечение.
Минимальное замкнутое множество, содержащее

, есть

.
Следовательно, пересечение есть

.
-- 25.08.2017, 12:04 --Определение 8.
Множество

называется
1) плотным в себе, если

;
2) совершенным, если

;
3) всюду плотным, если

.
Задача 20.
Множество плотно в себе, если и только если у него нет изолированных точек.
Доказательство.
Пусть множество

плотно в себе. Предположим, у него есть изолированные точки, и

-- одна из них.

не является предельной точкой (задача 7), т.е.

. Но тогда из

следует

-- противоречие с существованием изолированных точек.
Пусть теперь

-- множество, у которого нет изолированных точек. Все точки

являются предельными (задача 7), т.е.

.
-- 25.08.2017, 12:05 --Задача 21.
Множество совершенно, если и только если оно замкнуто и плотно в себе.
Доказательство.
Тривиально (я правильно употребляю это слово?):

.
-- 25.08.2017, 12:15 --По задаче 15.
Плохо сформулировано: во-первых, нехорошо обозначать разные точки одним и тем же игреком, а во-вторых, этот игрек всё равно нигде потом не используется. Надо было вместо выделенного написать просто "
т.е. принадлежащая 
".
Ок.
Если

не имеет предельных точек, то оно замкнуто (см. доказательство задачи 12).
Если это выкинуть, то всё станет совсем нормально. А эта фраза -- просто излишня: замкнутость ровно и означает, что множество содержит все свои предельные точки. Т.е. что из предельности точки следует её принадлежность множеству -- не более и не менее того.
Вторая часть тоже ок, но вот здесь:
Возьмем произвольное замкнутое множество

и покажем что произвольная точка

-- внутренняя.
нужно было вспомнить вырожденный случай, когда нет никакой точки

.
Мне кажется, или ваши с
ewert замечания противоречат друг другу?
Открытость означает, что из принадлежности точки множеству следует что эта точка внутренняя. Значит (по
ewert), случай отсутствия точек можно не рассматривать отдельно, так?