А мне вот дополнительно интересна и сложность алгоритма.
Да ужасающая там сложность.Например, если мы хотим проверить на простоту число порядка

(это совсем небольшое число по современным понятиям; например, программа Primo, использующая метод эллиптических кривых, на моём компьютере за

секунды проверила, что число

является простым, и выдала сертификат простоты, который можно проверить; это число сгенерировала Wolfram Mathematica командой
![$\mathbf{Timing[RandomPrime[{10^{100}, 2*10^{100}}]]}$ $\mathbf{Timing[RandomPrime[{10^{100}, 2*10^{100}}]]}$](https://dxdy-04.korotkov.co.uk/f/b/4/8/b485a4451b9fc50b52f56b6c2e83f4dd82.png)
за

секунды), то мы должны найти все простые числа, не превосходящие квадратный корень из проверяемого числа. Их нужно разбить на две группы (разбиение может быть произвольным) и перемножить числа в каждой группе (можно каждое взять в любой степени), что даст те самые

и

; произведение этих чисел никак не меньше, чем примориал

. Используя
оценку примориала 
, получаем, что произведение
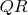
есть, как минимум, число порядка

. Таким образом, нам придётся иметь дело с числами, в десятичной записи которых примерно

цифр. Я думаю, что дальнейшее обсуждение сложности рассматриваемого алгоритма проверки простоты (одного!) числа не имеет смысла.



