Неадиабатический процесс в газе под поршнем в цилиндре

[reterty]

Я занимаюсь выводом уравнения неадиабатического процесса ($T(V)$) в газе, сжимающимся (расширяющимся) в цилиндре с определенной скоростью под поршнем с учетом ненулевой теплопроводности стенок в приближении равновесности процесса. Однако, расчет усложняется необходимостью учета теплоемкости стенок и поршня. Я не буду здесь выкладывать вывод диффура, описывающего процесс, а постараюсь изложить суть проблемы "на пальцах". Пусть, в определенный момент существует некоторый температурный профиль распределения температуры вдоль толщины стенок цилиндра и поршня. Если температура газа при изменении обьема меняется то наклон это профиля со временем должен меняться. Однако, за счет того что теплоемкость оболочки много больше теплоемкости газа при постоянном обьеме, то изменения температуры газа должны существенно "гаситься" (в этом приближении), т.е. процесс должен быть близок к изотермическому. Возможно, причина этого теорпарадокса кроется в неучете коэффициента теплоотдачи внутренних стенок неадиабатической оболочки...... Я провел выкладки, с учетом теплоотдачи. Вроде бы, этот фактор перенормировал безразмерное отношение теплоемкости оболочки к теплоемкости газа в сторону уменьшения этого параметра расчетной модели. Однако, я не задавался численными значениями коэффициента теплоотдачи. Действительно ли будет существенной такая перенормировка? Другими словами, устраняет ли этот учет парадокс?

[Pphantom]

Из описания совершенно непонятно, в чем состоит парадокс. Имеющийся текст можно понять так, будто Вы используете два разных предположения о теплоотдаче через стенки, тогда, естественно, результаты будут разными.

[reterty]

Pphantom в сообщении #1241618 писал(а):

Из описания совершенно непонятно, в чем состоит парадокс. Имеющийся текст можно понять так, будто Вы используете два разных предположения о теплоотдаче через стенки, тогда, естественно, результаты будут разными.

Вопрос в том похоже ли на "правду" то что учет теплоотдачи от внутренних стенок способен устранить эффект квазиизотермичности, который, в свою очередь, является следствием очень большой по сравнению с теплоемкостью газа теплоемкостью оболочки

[GraNiNi]

reterty в сообщении #1241599 писал(а):

Я занимаюсь выводом уравнения неадиабатического процесса ($T(V)$) в газе, сжимающимся (расширяющимся) в цилиндре с определенной скоростью под поршнем с учетом ненулевой теплопроводности стенок в приближении равновесности процесса.

Аналитическое решение такой задачи слишком сложно и практически невозможно - слишком много факторов, поэтому их решают численными методами (моделированием).
Да и сомнительно, что за вменяемое время сжатия газа, там будет равновесный процесс, если конечно это время не измеряется часами и сутками.

[DimaM]

Температуропроводность воздуха что-то вроде $0.15\,\mbox{см}^2/\mbox{с}$, так что для существенной отдачи тепла при быстром сжатии цилиндр должен быть достаточно тонким.

[reterty]

GraNiNi в сообщении #1241682 писал(а):

reterty в сообщении #1241599 писал(а):

Я занимаюсь выводом уравнения неадиабатического процесса ($T(V)$) в газе, сжимающимся (расширяющимся) в цилиндре с определенной скоростью под поршнем с учетом ненулевой теплопроводности стенок в приближении равновесности процесса.

Аналитическое решение такой задачи слишком сложно и практически невозможно - слишком много факторов, поэтому их решают численными методами (моделированием).
Да и сомнительно, что за вменяемое время сжатия газа, там будет равновесный процесс, если конечно это время не измеряется часами и сутками.

Уважаемый GraNiNi! численное моделирование газовых процессов в ДВС очень мощное но не единственное направление в технической термодинамике. Для оценки КПД и рабочих температур
также имеет место быть равновесная finite time thermodynamics (FTT) учитывающая в равновесном приближении теплообмен с холодильником и нагревателем. Взять хотя бы ее знаментую формулу (формула Курзона-Эшборна) для КПД цикла Карно: $\eta=1-\sqrt{T_{x}/T_{n}}$, полученную в предположении максимальной мощности двигателя.

-- Сб авг 19, 2017 18:56:34 --

DimaM в сообщении #1241773 писал(а):

Температуропроводность воздуха что-то вроде $0.15\,\mbox{см}^2/\mbox{с}$, так что для существенной отдачи тепла при быстром сжатии цилиндр должен быть достаточно тонким.

Уважаемый DimaM! Правильно ли я понимаю, что реальное неравновесное осевое и радиальное мгновенное распределение температур в цилиндре можно заменить равновесным с феноменологическими коэффициентами теплоотдачи?

[amon]

Если речь идёт о ДВС, то в нем, насколько я помню, основной механизм теплопередачи (охлаждение поршня) это тепловой поток от поршня к стенкам цилиндра через поршневые кольца. По этой причине при поломке верхнего поршневого кольца часто происходит оплавление огневой поверхности поршня.

[GraNiNi]

reterty в сообщении #1241783 писал(а):

Взять хотя бы ее знаментую формулу (формула Курзона-Эшборна) для КПД цикла Карно: $\eta=1-\sqrt{T_{x}/T_{n}}$, полученную в предположении максимальной мощности двигателя.

Наверное имеется ввиду формула Новикова-Курзона-Альборна.

Но это к делу отношения не имеет.

Повторю, аналитически рассчитать реальный процесс сжатия газа в двигателях, теплопередачу через стенки цилиндров и поршень, а также потери тепла с наружной поверхности цилиндра путем излучения и конвекции - невозможно.

Поэтому непонятно, что Вы хотите рассчитать

reterty в сообщении #1241599 писал(а):

Я занимаюсь выводом уравнения неадиабатического процесса

[reterty]

Хорошо. Я приведу выкладки (надеюсь, с английским проблем не возникнет) а затем еще раз сформулирую вопрос.
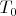
Let us consider cylinder with base area $S$ inside which there is the ideal gas under the piston with the amount of the substance $\nu$. The temperature of the outer surfaces of the system is kept constant and equal to $T_{0}$. Let at the certain time moment the speed of piston motion is equal to $\upsilon $.

Let us write the first law of thermodynamics in the differential form:
$dU=\delta Q-pdV.$
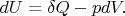
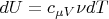
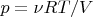
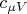
But $dU=c_{\mu V}\nu dT$, $p=\nu RT/V$, $dV=\pm S\upsilon dt$, where $c_{\mu V}$ is the molar heat capacity at constant volume, $R$ is the gas constant. The upper (lower) sign in the last equality relates to expansion (compression) of gas. From these relations we have: $(c_{\mu } -c_{\mu V} )dT=\pm\frac{RTS\upsilon dt}{V}.$
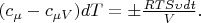
According to the low of conservation of energy the amount of heat taken away from the gas, is partially transferred to the environment and is partially spent on the heating of system piston-cylinder: $-\delta Q=\delta Q_{\rm transfer} +\delta Q_{\rm capasity}.$


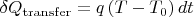
Using Fourier's law we have: $\delta Q_{\rm transfer}=q\left(T-T_0\right)dt$. The quantity $q$ has independent and dependent on gas volume (time moment) parts. The constant part is associated with flat piston and bottom of cylinder. The time dependent part caused by the piston motion and is associated with the cylindrical wall which actual height changes in time.

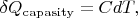
As it is well-known $\delta Q_{\rm capasity}=CdT,$ where $C>0$ is the total heat capacity of the non-adiabatic shell. This quantity has also independent and dependent from gas volume parts which in its turn have the same origin as well as above mentioned parts of $q$.
Using these expressions we derive the differential equation describing our process:
$\frac{dT}{dV} =-\left( \frac{\gamma-1} {1+r}\right)\frac{T}{V} \mp\frac{T-T_{0}}{(1+r)V_0} $,
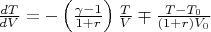
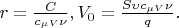
where $r=\frac{C}{c_{\mu V}\nu}, V_{0}=\frac{S\upsilon c_{\mu V}\nu }{q}. $ (1)

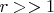
А теперь вопрос: В знаменателе правой части уравнения (1) фигурирует безразмерный параметр $r>>1$. Четко видно, что он сильно "тушит" изменения температуры при изменении обьема. Но я же видел собственными глазами возгорание ваты, смоченной спиртом при однократном сжатии поршня в опыте с воздушным огнивом.....

[GraNiNi]

reterty в сообщении #1241854 писал(а):

Я приведу выкладки

Лучше дайте ссылку на эту статью.

reterty в сообщении #1241854 писал(а):

Но я же видел собственными глазами возгорание ваты, смоченной спиртом при однократном сжатии поршня в опыте с воздушным огнивом.....

Потому что реальный процесс в цилиндре - сильно неравновесный, и за ту долю секунды, что сжимается газ, он успевает нагреться до высокой температуры, а теплоперенос через стенки не успевает его охладить.

В связи с этим, все приведенные выкладки, к реальному, неравновесному процессу не имеют никакого отношения.

[reterty]

GraNiNi в сообщении #1241917 писал(а):

reterty в сообщении #1241854 писал(а):

Я приведу выкладки

Лучше дайте ссылку на эту статью.

reterty в сообщении #1241854 писал(а):

Но я же видел собственными глазами возгорание ваты, смоченной спиртом при однократном сжатии поршня в опыте с воздушным огнивом.....

Потому что реальный процесс в цилиндре - сильно неравновесный, и за ту долю секунды, что сжимается газ, он успевает нагреться до высокой температуры, а теплоперенос через стенки не успевает его охладить.

В связи с этим, все приведенные выкладки, к реальному, неравновесному процессу не имеют никакого отношения.

Статья на рецензировании у третьего (тритейского) рецензента. Мнения двух первых разошлись. По поводу неравновесности процесса: Модель, описанная выше применима к любому равновесному процессу, пусть даже протекающему с большой скоростью. В выражении (1) скорость движения поршня "сидит" в $V_0$. При очень большой скорости движения поршня второе слагаемое "зануляется", т.е. тепло не успевает "отводиться" наружу. Но остается перенормированное $r$ первое слагаемое, т.е. вся теплота идет изменение температурного профиля в стенках оболочки, за счет чего (большая теплоемкость оболочки) процесс продолжает оставаться квазиизотермичским.....
Таким образом должен быть механизм, котолрый препятствует и нагреванию оболочки при быстром движении поршня (теплоотдача внутренних стенок????)

-- Вс авг 20, 2017 15:52:16 --

....И большое спасибо за уточнение о Новикове (1957 год)-основоположнике оптимизационной термодинамики

[GraNiNi]

reterty в сообщении #1241935 писал(а):

Модель, описанная выше применима к любому равновесному процессу, пусть даже протекающему с большой скоростью.

Если с большой скоростью - то равновесным он не может быть никак.
Кроме того, в теплопередаче через стенку должна фигурировать не только теплоемкость, но и ее теплопроводность, чего в этих формулах не наблюдается.

И все равно не понятно - что Вы хотите получить?
Распределение температуры в стенке цилиндра после сжатия газа?

[amon]

По поводу выкладок. Какая-то там, IMHO, лажа. В формуле

reterty в сообщении #1241854 писал(а):

$(c_{\mu } -c_{\mu V} )dT=\pm\frac{RTS\upsilon dt}{V}.$

величина $c_{\mu }$ будет константой только для политропы. Поскольку ни кто не сказал, что процесс политропический, то в общем случае $c_{\mu }$ это функция от температуры и, скажем, объёма. Уравнение

reterty в сообщении #1241854 писал(а):

$\delta Q_{\rm transfer}=q\left(T-T_0\right)dt$

справедливо только для области между двумя плоскостями, поверхности которых имеют постоянные температуры. К процессу теплопередачи в цилиндре это соотношение не имеет никакого отношения. Соотношение

reterty в сообщении #1241854 писал(а):

$\delta Q_{\rm capasity}=CdT$

справедливо только когда $dT$ это изменение температуры цилиндра. При этом температура цилиндра не обязана равняться температуре газа и вообще, быть постоянной.

[GraNiNi]

reterty в сообщении #1241935 писал(а):

Таким образом должен быть механизм, котолрый препятствует и нагреванию оболочки при быстром движении поршня (теплоотдача внутренних стенок????)

Этот механизм - конвективная теплоотдача от газа к стенкам цилиндра.
Коэффициент же этой теплоотдачи аналитически не выводится, а вычисляется через критерий Нуссельта и прочие коэффициенты подобия.

[reterty]

amon в сообщении #1241960 писал(а):

По поводу выкладок. Какая-то там, IMHO, лажа. В формуле

reterty в сообщении #1241854 писал(а):

$(c_{\mu } -c_{\mu V} )dT=\pm\frac{RTS\upsilon dt}{V}.$

величина $c_{\mu }$ будет константой только для политропы. Поскольку ни кто не сказал, что процесс политропический, то в общем случае $c_{\mu }$ это функция от температуры и, скажем, объёма. Уравнение

reterty в сообщении #1241854 писал(а):

$\delta Q_{\rm transfer}=q\left(T-T_0\right)dt$

справедливо только для области между двумя плоскостями, поверхности которых имеют постоянные температуры. К процессу теплопередачи в цилиндре это соотношение не имеет никакого отношения. Соотношение

reterty в сообщении #1241854 писал(а):

$\delta Q_{\rm capasity}=CdT$

справедливо только когда $dT$ это изменение температуры цилиндра. При этом температура цилиндра не обязана равняться температуре газа и вообще, быть постоянной.

Уважаемый amon! 1) Теплоемкость у меня в общем случае и не предполагается постоянной. До тех пор пока начнется интегрирование уравнения (1). Я нашел решение этого уравнения в спецфункциях (различного типа для расширения и сжатия). Это уравнение (1) "выкручивается" из вышеупомянутых по тексту соотношений и теплоемкость там не фигурирует ("уходит"). 2) Да, вместо численного решения нестационарного уравнения теплопроводности используется "мгновенный " закон Фурье, поскольку если процесс в газе равновесный то процесс передачи тепла через оболочку и подавно будет стационарным: сравните теплопроводности)). По сути, отказываясь от квазистацонарности процесса передачи тепла вы "хороните" целое направление -finite time thermodynamics. Которое , хотя и оценочное но тоже имеет право на жизнь. 3) По поводу теплоемкости оболочки: это , естественно есть величина эффективная, поскольку температура меняется вдоль толщины стенок. Она меньше истинной но не на порядок! К примеру, в предположении линейного профиля - в два раза меньше.