Хорошо. Я приведу выкладки (надеюсь, с английским проблем не возникнет) а затем еще раз сформулирую вопрос.
Let us consider cylinder with base area
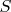
inside which there is the ideal gas under the piston with the amount of the substance

. The temperature of the outer surfaces of the system is kept constant and equal to
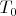
. Let at the certain time moment the speed of piston motion is equal to

.
Let us write the first law of thermodynamics in the differential form:
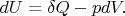
But
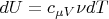
,
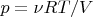
,

, where
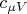
is the molar heat capacity at constant volume,
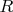
is the gas constant. The upper (lower) sign in the last equality relates to expansion (compression) of gas. From these relations we have:
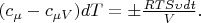
According to the low of conservation of energy the amount of heat taken away from the gas, is partially transferred to the environment and is partially spent on the heating of system piston-cylinder:

Using Fourier's law we have:
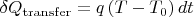
. The quantity
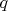
has independent and dependent on gas volume (time moment) parts. The constant part is associated with flat piston and bottom of cylinder. The time dependent part caused by the piston motion and is associated with the cylindrical wall which actual height changes in time.
As it is well-known
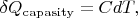
where
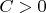
is the total heat capacity of the non-adiabatic shell. This quantity has also independent and dependent from gas volume parts which in its turn have the same origin as well as above mentioned parts of
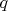
.
Using these expressions we derive the differential equation describing our process:
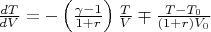
,
where
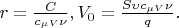
(1)
А теперь вопрос: В знаменателе правой части уравнения (1) фигурирует безразмерный параметр
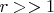
. Четко видно, что он сильно "тушит" изменения температуры при изменении обьема. Но я же видел собственными глазами возгорание ваты, смоченной спиртом при однократном сжатии поршня в опыте с воздушным огнивом.....