Someone писал(а):
Если Вы изучаете математику, для Вас не должно быть удивительным, что предел последовательности и предел функции имеют специальные определения.
Эти определения мне известны и прекрасно понятны.
Someone писал(а):
Предел множеств или предел геометрических фигур также нужно сначала определить, а потом уже о нём говорить. Причём, если определения предела последовательности или предела функции являются, в общем-то, общепринятыми, то о пределе множеств или пределе геометрических фигур этого, вообще говоря, сказать нельзя. Это же Вам и ET пишет.
Я сознательно употребил такое, недопустимое из-за нестрогости, выражение. Оправдываю это тем, что
Цитата:
В данном случае достаточно просто, поскольку любой паучок из последовательности однозначно определяется одной координатой и размером.
Someone писал(а):
Боюсь, что нет. Важно ещё его расположение на плоскости.
Длинные ноги всех паучков лежат на одной прямой. Сделаем эту прямую координатной осью, зафиксировав направление и точку отсчёта. Тогда положение центра паучка можно задать одной действительной координатой, а размер и (одно из двух возможных) направление — вектором из центра паучка к концу длинной ноги — также действительным числом. Теперь слова "последовательность паучков" заменяются на "последовательность положений центров
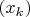
и последовательность "размеров"

". Легко увидеть, что они сходятся: первая к конечному числу, а вторая — к нулю. Это было описано словами "предел последовательности паучков — точка".
Отмечу, что то множество

, которое я хотел построить, содержит эту точку, то есть уже не пусто.
Ну да ладно. Хоть удевлетворяюще чёткого определения множеству я и
не дал, но зато сам понял, то, что
хотел понять.
Паучков в

нет, поскольку они в пределе вырождаются в точки. А самих этих точек в

континуальное количество.
Спасибо всем, кто учавствовал.
P.S.
Someone писал(а):
Бесконечным последовательностям неоткуда взяться.
Не могли бы Вы посоветовать литературу, которая объясняет тонкости анализа математических объектов, построенных с использованием понятия "бесконечность"?
А потом, я думаю, можно и тему закрыть
 Добавлено спустя 1 минуту 8 секунд:
Добавлено спустя 1 минуту 8 секунд:Профессор Снэйп писал(а):
У меня стойкое ощущение, что ulidtko есть ни что иное, как очередная инкарнация Давидюка.
Почему?
