Мне интересно существуют ли какие-либо точки (кроме

) на расстояний

от

Может быть да, может быть нет: это зависит от того, какое именно метрическое пространство вы рассматриваете. Если

или

, то ответ
да.
Пусть

конечное метрическое пространсто
Что значит конечное метрическое пространство? Состоит из конечного количества точек?
Имеет ли тогда смысл говорить, что
a. окрестность

- это интервал в

зависящий от

Нет, не имеет. Во-первых, что такое "интервал"? Во-вторых, откуда взялось какое-то

?
некоторые точки

попадают в этот интервал, некоторые находятся за его пределами
Да: если выбрать какую-то окрестность точки

, то, вообще говоря, некоторые точки метрического пространства ей принадлежат, а некоторые нет. Но всё пространство -- тоже окрестность любой своей точки (впрочем, определения окрестности бывают разные, напишите свой вариант).
каждая окрестность

находится в

Да, если "находится в

" понимать как "является подмножеством

".
Для справки:
открытый шар с центром

радиуса

(где

) -- это множество точек, удалённых от

менее чем на

. Я думаю, что именно это у вас обозначается
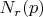
. Подмножество метрического пространства
открыто, если вместе с каждою своею точкою содержит также некоторый шар с центром в ней.
Окрестностью точки

обычно называется открытое множество, содержащее

.



