3dmnozhestvotochek, думаю, никто не будет против, если я напишу решение похожей задачи.
Можно ли выразить
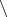
через

и

?
Ответ: нельзя.
Доказательство: докажем, что любое множество, которое можно получить из

и

с помощью

и

содержит все элементы, содержащиеся в

.
Будем доказывать индукцией по числу операций в выражении.
База:

операций - наше выражение либо

либо

, для него утверждение выполнено.
Шаг: пусть нельзя выразить формулой, содержащей меньше чем

операций. Рассмотрим какую-нибудь формулу, содержащую

операций. Последняя (внешняя) операция - либо

, либо

. Если это

, то формула имеет вид

, где

и

получены из

и

с помощью менее чем

операций. Следовательно,

и

содержат

как подмножество, и то же выполнено для

. Аналогично для формулы

.
Рассмотрим теперь

. Тогда

. Следовательно, выразить

с помощью

и

нельзя.
Не нужна тут никакая математическая индукция.
Если расписывать строго, то индукция по длине формулы / числу операций нужна.



