Разложение волновой функции - 2

[Gickle]

rank_xyz в сообщении #1237948 писал(а):

состояние частицы хоть и описывается при таком разложении двумя функциями

Состояние (чистое) описывается одной волновой функцией (пусть $\Psi$). Разложение волновой функции $\Psi$ по собственным функциям $\varphi_n$ какого-либо эрмитова оператора есть не что иное, как разложение вектора по базису. Заметьте, что, как вам уже не раз говорили, здесь нигде не идёт речь о том, является ли функция $\Psi$ СФ какого-либо оператора. Поэтому, разумеется, можно и собственную функцию оператора импульса разложить по собственным функциям оператора координаты. При этом, как уже опять же говорилось, окажется, что все коэффициенты в разложении ненулевые и равны между собой, что и означает, что такое состояние полностью делокализовано. В полном соответствии с принципом неопределённости.

P.S. В вашей мешанине слов вообще очень сложно что-либо разобрать. То есть значительная часть слов по отдельности имеет смысл, но в совокупности написанное вами представляет по большей части бред. Вы можете нормально написать (не словами), как в квантовой механике волновая функция может быть разложена по СФ оператора какой-либо физической наблюдаемой и какой физический смысл имеет всё написанное?

[Dragon27]

rank_xyz в сообщении #1237956 писал(а):

или при разложении волновой функции свободной частицы по собственным функциям оператора координаты информация о собственном значении импульса необратимо утрачивается? но разве тогда можно это разложение назвать корректным?

Если вы разложили так, что у вас утратилась информация, то вы разложили, разумеется, некорректно.
Вон у меня выше есть удобная ссылка на то, как будет выглядеть собственное состояние оператора импульса в двух представлениях (это одно состояние), и собственное состояние оператора координаты в двух представлениях (это уже совершенно другое состояние).
В ваших выкладках я вообще не увидел, чтобы вы в конечном итоге поменяли представление. У меня такое ощущение, что вы просто выдрали один коэффициент из разложения и посчитали его за исходную функцию (а как же остальные бесконечное количество коэффициентов?). Если вы возьмёте собственную функцию одного оператора и представите его в базисе другого оператора (с которым первый не коммутирует), у вас не должна получиться собственная функция другого оператора.

[rank_xyz]

Gickle в сообщении #1237957 писал(а):

rank_xyz в сообщении #1237948 писал(а):

состояние частицы хоть и описывается при таком разложении двумя функциями

Состояние (чистое) описывается одной волновой функцией (пусть $\Psi$). Разложение волновой функции $\Psi$ по собственным функциям $\varphi_n$ какого-либо эрмитова оператора есть не что иное, как разложение вектора по базису. Заметьте, что, как вам уже не раз говорили, здесь нигде не идёт речь о том, является ли функция $\Psi$ СФ какого-либо оператора. Поэтому, разумеется, можно и собственную функцию оператора импульса разложить по собственным функциям оператора координаты. При этом, как уже опять же говорилось, окажется, что все коэффициенты в разложении ненулевые и равны между собой, что и означает, что такое состояние полностью делокализовано. В полном соответствии с принципом неопределённости.

коэффициентами разложения любой функции в координатном представлении по собственным функциям оператора координаты в координатном же представлении являются, вообще то, сами значения исходной волновой функции
т.е. все значения волновой функции свободной частицы равны друг другу в любой точке пространства и в любой момент времени при определенном значении импульса?

-- 03.08.2017, 12:32 --

Dragon27 в сообщении #1237959 писал(а):

rank_xyz в сообщении #1237956 писал(а):

или при разложении волновой функции свободной частицы по собственным функциям оператора координаты информация о собственном значении импульса необратимо утрачивается? но разве тогда можно это разложение назвать корректным?

Если вы разложили так, что у вас утратилась информация, то вы разложили, разумеется, некорректно.
Вон у меня выше есть удобная ссылка на то, как будет выглядеть собственное состояние оператора импульса в двух представлениях (это одно состояние), и собственное состояние оператора координаты в двух представлениях (это уже совершенно другое состояние).
В ваших выкладках я вообще не увидел, чтобы вы в конечном итоге поменяли представление. У меня такое ощущение, что вы просто выдрали один коэффициент из разложения и посчитали его за исходную функцию (а как же остальные бесконечное количество коэффициентов?). Если вы возьмёте собственную функцию одного оператора и представите его в базисе другого оператора (с которым первый не коммутирует), у вас не должна получиться собственная функция другого оператора.

сам ничего не раскладываю, просто анализирую вопросы и ответы отсюда
автор вопроса не меняет представление
но судя по тому разложению, информация об импульсе будет утрачена

[Gickle]

rank_xyz
Разумеется, я просто неаккуратно выразился и надо было сказать, что равны не коэффициенты, а их абсолютные величины. А вы бы лучше начали всё-таки что-нибудь по существу писать, а не только повторять одну и ту же мантру.

[Dragon27]

rank_xyz в сообщении #1237961 писал(а):

но судя по тому разложению, информация об импульсе будет утрачена

У него какая функция вначале была, такая в конце и осталась (неудивительно, если он раскладывал функцию в координатном представлении в координатное представление). Просто записано через интеграл: $f(x)=\int f(y) \delta(x-y) dy$.

[Pphantom]

rank_xyz, в данной теме Вам были заданы многочисленные вопросы, ответы на которые следует все-таки дать. В противном случае тема поедет в Пургаторий.

[rank_xyz]

Dragon27 в сообщении #1237966 писал(а):

rank_xyz в сообщении #1237961 писал(а):

но судя по тому разложению, информация об импульсе будет утрачена

У него какая функция вначале была, такая в конце и осталась (неудивительно, если он раскладывал функцию в координатном представлении в координатное представление). Просто записано через интеграл: $f(x)=\int f(y) \delta(x-y) dy$.

тогда как быть с собственными значениями координаты и импульса, а также с собственными функциями соответствующих операторов?
есть тут ошибки в рассуждениях?

[Dragon27]

rank_xyz в сообщении #1237970 писал(а):

есть тут
ошибки в рассуждениях?

У вас там (как я уже говорил) непонятно, как вы начальную функцию приравняли дельта-функции от координаты (собственная функция оператора координат). Эта дельта функция лишь часть разложения изначальной функции по всему континууму, и полностью функция представляет собой сумму по всем этим дельтам с соответствующими коэффициентами. Разумеется, если выдрать только одну дельта, то она при измерении будет давать стопроцентно только одно значение координаты, а если измерять импульс уже с полной изначальной функции, то она будет давать стопроцентное значение конкретного импульса. Но если измерять координату с полноценной (начальной) функции, то она уже не будет давать только одно значение координаты (а если замерять импульс только с одной дельта-функции координаты, а не сразу со всей суммы-интеграла всех дельта-функций, то мы не получим изначальное конкретное значение импульса). Вы после разложения оставили только часть информации, а всё остальное зачем-то выкинули.

PS:
мне кажется, что я уже достаточно наобъяснял (даже сам начал понимать (с) ), так что дальше продолжать не буду

[Alex-Yu]

rank_xyz в сообщении #1237934 писал(а):

4) из п.1 и 2 следует, что любое совместное измерение импульса и координаты в состоянии $\varphi_m$ с вероятностью 1 даст собственные значения импульса $p_n$ и координаты $r_m$, что противоречит принципу неопределенности

Не следует. Функция с определенным импульсом не является функцией с определенной координатой (какой-то одной, с единственным $r_n$), а является суперпозицией многих функций с разными координатами $r_n$. Квадрат модуля одного из коэффициентов в этой суперпозиции (любого), кстати, дает вероятность того, что координата равна этому конкретному $r_n$. Эта величина отлична от нуля для самых разных $r_n$, что и означает, что при измерении координаты могут получаться разные $r_n$.


А вообще это все уже надоело. Из дискуссии явно следует, что rank_xyz этого не поймет никогда. Ну не умеет он логически мыслить, что тут поделать... Если уж он не видит разницы между линейной комбинацией многих разных функций с разными определенными координатами и одной единственной функцией с одной единственной определенной координатой... Можно только порекомендовать поискать себя в какой-то иной области.

-- Чт авг 03, 2017 16:29:15 --

Alex-Yu в сообщении #1237973 писал(а):

Из дискуссии явно следует, что rank_xyz этого не поймет никогда.

Впрочем, последняя попытка. Пусть есть две волновые функции с определенной координатой:

$$ \phi_1(r)=\delta(r-r_1) $$

и

$$ \phi_2(r)=\delta(r-r_2) $$

$$ r_1 \ne r_2 $$

Делаем из них третью волновую функцию:

$$ \psi_3(r)=\frac{1}{\sqrt{2}}(\psi_1(r)+\psi_2(r)) $$

rank_xyz, как по-вашему, является ли определенной, и если да, то чему равна координата $r$ в состоянии, описываемом функцией $\psi_3$? Если не сможете ответить правильно на этот вопрос, то Вам точно в физике делать нечего, не стОит даже и пытаться.

[rank_xyz]

Walker_XXI в сообщении #1237813 писал(а):

Не наводите тень на плетень :)
В вопросе идёт речь об обычном разложении в ряд Фурье (да, импульсное и координатное представления связаны преобразованием Фурье, разложение в ряд будет иметь место для частицы в ограниченной области, когда набор собственных функций дискретный, а так это преобразование Фурье). В общем случае - разложение по полной системе функций. Здесь нет ничего загадочного и ничто при таком разложении не теряется (равенство математически строгое, если система функций полная).

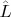
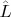
При этом тот объект, который Вы обозначаете $\Psi_{nm}$, является произведением скалярного коэффициента (скалярного произведения $\left\langle\Phi_m,\psi_n\right\rangle$) на $\Phi_m$ - собственную функцию оператора координаты (или $\hat{L}$, как тут выше стали писать). C какой стати он должен оказаться ещё и собственной функцией оператора импульса, не коммутирующего с $\hat{L}$? Если настаиваете на своём - докажите :).
Ерунду пишете. Как я отметил выше, $c_{nm}$ - это скалярное произведение функций, комплексное число. Называть его функцией в данном контексте язык не поворачивается. :)) (Доп. Тут я, пожалуй, перегнул палку. Всё-таки функция, но другим переменным, по отношению к оператору - скаляр.

разве разложение функции какого то оператора по собственным функциям другого оператора должно менять свойства исходной функции? тем более, если представление исходной функции не меняется?
если идет разложение собственной функции оператора импульса по собственным функциям оператора координаты (все в координатном представлении), и в итоге остаются только собственные функции оператора координаты, то получается, что информация об исходной функции теряется, что намекает на некорректность разложения
вид исходной функции не должен искажаться, может измениться разве что представление!

Walker_XXI в сообщении #1237813 писал(а):

Докажите. Продемонстрируйте публике, что функции $\Psi(r,t)=Ae^{\frac{i}{\hbar}(\operatorname{pr}-Et)}$
и $\varphi_{r_n}=\delta(r-r_n)$ обе являются собственными функциями и оператора импульса, и оператора координаты.

Другое дело, что для свободной частицы в неограниченном пространстве речь должна идти о непрерывном спектре и о преобразовании Фурье, а не разложении в ряд.

зачем мне доказывать то, чего не утверждаю?
автор вопроса раскладывает собственную функцию оператора импульса в координатном представлении по собственным функциям оператора координаты, который тоже в координатном представлении
что же должно получиться в итоге?
если оператор импульса и оператор координаты не имеют общих функций, то куда в итоге денется собственная функция оператора импульса?
судя по разложению, она переезжает в $C_n$
о чем и упоминалось

Walker_XXI в сообщении #1237813 писал(а):

Речь идет о разложении функции по полной системе других функций. При чём тут произведение операторов и их коммутатор?

произведение операторов в Квантовой механике Ландау трактуется как последовательное применение операторов, что не так?
коммутатор у меня вообще не упоминался

-- 03.08.2017, 14:22 --

Dragon27 в сообщении #1237971 писал(а):

rank_xyz в сообщении #1237970 писал(а):

есть тут
ошибки в рассуждениях?

У вас там (как я уже говорил) непонятно, как вы начальную функцию приравняли дельта-функции от координаты (собственная функция оператора координат). Эта дельта функция лишь часть разложения изначальной функции по всему континууму, и полностью функция представляет собой сумму по всем этим дельтам с соответствующими коэффициентами. Разумеется, если выдрать только одну дельта, то она при измерении будет давать стопроцентно только одно значение координаты, а если измерять импульс уже с полной изначальной функции, то она будет давать стопроцентное значение конкретного импульса. Но если измерять координату с полноценной (начальной) функции, то она уже не будет давать только одно значение координаты (а если замерять импульс только с одной дельта-функции координаты, а не сразу со всей суммы-интеграла всех дельта-функций, то мы не получим изначальное конкретное значение импульса). Вы после разложения оставили только часть информации, а всё остальное зачем-то выкинули.

PS:
мне кажется, что я уже достаточно наобъяснял (даже сам начал понимать (с) ), так что дальше продолжать не буду

прошу прощения, какую часть выкинул?

-- 03.08.2017, 14:34 --

Alex-Yu в сообщении #1237973 писал(а):

Не следует. Функция с определенным импульсом не является функцией с определенной координатой (какой-то одной, с единственным $r_n$), а является суперпозицией многих функций с разными координатами $r_n$. Квадрат модуля одного из коэффициентов в этой суперпозиции (любого), кстати, дает вероятность того, что координата равна этому конкретному $r_n$. Эта величина отлична от нуля для самых разных $r_n$, что и означает, что при измерении координаты могут получаться разные $r_n$.

хорошо, чем определяется значение импульса для каждой конкретной функции с конкретной координатой? и чему равна вероятность получить в результате измерений значение координаты $r_n$, если состояние описывается функцией $\delta(r-r_n)$?

Alex-Yu в сообщении #1237973 писал(а):

А вообще это все уже надоело. Из дискуссии явно следует, что rank_xyz этого не поймет никогда. Ну не умеет он логически мыслить, что тут поделать... Если уж он не видит разницы между линейной комбинацией многих разных функций с разными определенными координатами и одной единственной функцией с одной единственной определенной координатой... Можно только порекомендовать поискать себя в какой-то иной области.

-- Чт авг 03, 2017 16:29:15 --

Alex-Yu в сообщении #1237973 писал(а):

Из дискуссии явно следует, что rank_xyz этого не поймет никогда.

Впрочем, последняя попытка. Пусть есть две волновые функции с определенной координатой:

$$ \phi_1(r)=\delta(r-r_1) $$

и

$$ \phi_2(r)=\delta(r-r_2) $$

$$ r_1 \ne r_2 $$

Делаем из них третью волновую функцию:

$$ \psi_3(r)=\frac{1}{\sqrt{2}}(\psi_1(r)+\psi_2(r)) $$

rank_xyz, как по-вашему, является ли определенной, и если да, то чему равна координата $r$ в состоянии, описываемом функцией $\psi_3$? Если не сможете ответить правильно на этот вопрос, то Вам точно в физике делать нечего, не стОит даже и пытаться.

координата в состоянии $\psi_3$ не определена, но речь то о том, что если в момент измерения состояние было $\psi_1$, например, то вероятность получить при измерении значение $r_1$ равно 1
что не так?

[Alex-Yu]

rank_xyz в сообщении #1237986 писал(а):

координата в состоянии $\psi_3$ не определена

Замечательно! А в случае, когда раскладывается собственная функция импульса все точно также, лишь слагаемых не два, а бесконечно много. Так что Ваш "логический вывод" о том, что нарушается соотношение неопределенности и не вывод, и не логический. Ничего не нарушается.

-- Чт авг 03, 2017 17:48:01 --

rank_xyz в сообщении #1237986 писал(а):

но речь то о том, что если в момент измерения состояние было $\psi_1$, например, то вероятность получить при измерении значение $r_1$ равно 1
что не так?

То не так, что разложение функции с определенным импульсом НИ В КОЕМ СЛУЧАЕ не является одной единственной функцией $\psi_1$, а является суммой разных функций такого типа. И причем здесь тогда "если в момент измерения состояние было $\psi_1$". Если в момент измерения $\psi_1$, то это ни в коем случае НЕ РАЗЛОЖЕНИЕ функции с определенным импульсом.

[rank_xyz]

Alex-Yu в сообщении #1237993 писал(а):

rank_xyz в сообщении #1237986 писал(а):

координата в состоянии $\psi_3$ не определена

Замечательно! А в случае, когда раскладывается собственная функция импульса все точно также, лишь слагаемых не два, а бесконечно много. Так что Ваш "логический вывод" о том, что нарушается соотношение неопределенности и не вывод, и не логический. Ничего не нарушается.

-- Чт авг 03, 2017 17:48:01 --

rank_xyz в сообщении #1237986 писал(а):

но речь то о том, что если в момент измерения состояние было $\psi_1$, например, то вероятность получить при измерении значение $r_1$ равно 1
что не так?

То не так, что разложение функции с определенным импульсом НИ В КОЕМ СЛУЧАЕ не является одной единственной функцией $\psi_1$, а является суммой разных функций такого типа. И причем здесь тогда "если в момент измерения состояние было $\psi_1$". Если в момент измерения $\psi_1$, то это ни в коем случае НЕ РАЗЛОЖЕНИЕ функции с определенным импульсом.

не соглашусь
1) изначально в волновой функции свободной частицы координата не определена
2) после разложения волновой функции свободной частицы по собственным функциям оператора координаты появляются состояния $\varphi_m=\delta(r-r_m)$, в которых координата определена и равна собственному значению $r_m$
3) измерение координаты в состоянии $\varphi_m=\delta(r-r_m)$ с вероятностью 1 должно дать значение $r_m$
против этого возражения есть?

[Alex-Yu]

rank_xyz в сообщении #1237999 писал(а):

не соглашусь

Ну и хрен с тобой, придурок! Не соглашайся в одиночестве. И дальше сам свою бредятину читай (именно бердятина, ничто иное, на логику и намека нет, бессмысленный набор слов).

[Someone]

rank_xyz в сообщении #1237999 писал(а):

после разложения волновой функции свободной частицы по собственным функциям оператора координаты появляются состояния $\varphi_m=\delta(r-r_m)$, в которых координата определена и равна собственному значению $r_m$

Но частица в этих состояниях не находится, поэтому дальнейшие рассуждения ни на чём не основаны.

Но продолжать обсуждение бессмысленно, поскольку наблюдается троллинг, при котором тролль прикидывается дурачком.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Пургаторий (Ф)»

-- 03.08.2017, 14:32 --

rank_xyz, предупреждение за агрессивное невежество.
Alex-Yu, предупреждение за хамство.