kolodenВ Тейлор-Уилер гиперболические функции, которые мне в диковинку. Я себе сделал памятку "геометрический смысл гиперболических функций" из математического справочника. Аргумент

это удвоенная площадь фигуры, ограниченной отрезками

,
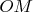
и кривой

, это и для окружности, и для гиперболы.

Вот ещё примеры. На Рис. 1 ранешний пример для наглядности (
post1228357.html#p1228357). На нём мировая линия тела
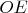
похожа на график движения точки

. И обратите внимание, что оси

симметричны относительно желтой линии - мировой линии света. Свяжем с телом другую инерциальную систему отсчета (ИСО) и назовем её штрихованной (Рис. 2). Ось времени

совпадает с мировой линией тела

. Ось

проведем симметрично относительно желтой линии. Событие "Синяя точка" спроектируем на оси

косыми проекционными линиями, параллельными этим осям. Симметрия сохраняется, в штрихованной ИСО свет пролетел расстояние

за время

. Если сопоставить Рис. 2 и Рис. 1, то напоминает пантограф на крыше электровоза. Пусть другое тело летит со скоростью

относительно штрихованной ИСО. Косой проекционный пунктир делим пополам и проводим мировую линию, подобно Рис. 1, но в косых координатах

. На самом верхнем прямом пунктире мировая линия тела отмечает точку

от его длины, это скорость тела относительно нештрихованной ИСО. Так складываются скорости. На Рис. 3 подобный пример для скоростей

.

Разметка осей (Рис. 4). Штрихованная ИСО летит со скоростью

. Пусть в неподвижной ИСО лежит стержень длиной 1 метр, одним концом в нуле. Мировые линии его концов вертикальные, одна совпадает с осью

, другая - отрезок

. Событие

в штрихованной ИСО одновременно с сбытием

, т. к. лежит на оси

, а отрезок

символизирует длину стержня в штрихованной ИСО. Но из-за сокращения эта длина меньше собственной длины стержня и равна

, т.е.

.
Чтобы получить единичную отметку на оси

, нужно стержень взять заведомо подлиннее

Мировая линия дальнего конца этого стержня

. Отрезок
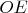
символизирует единичный отрезок на оси

. Рис. 5 частично повторяет Рис. 4, но там в каждой ИСО лежит метровый стержень, и показаны мировые линии обоих стержней, они параллельны соответствующим осям времени. Каждый стержень виден в другой ИСО укороченным до

.

Посмотрим на Рис. 4 как на евклидовый. Длина отрезка

. Из симметрии длина

. Найдем координаты точки

:


Возведем оба равенства в квадрат:


Вычтем из первого второе:

Получили уравнение гиперболы, она нарисована на Рис. 4. В уравнении нет скорости

, гипербола годится для разметки любых осей. Точка пересечения гиперболы с осью даёт единичную засечку.
На Рис. 6 Парадокс близнецов.
"Косые" оси и "растяжка" единичных отрезков - это плата за то, что абстрактное псевдоевклидово пространство нарисовано на реальной евклидовой бумаге.



