В общем. Надолго же я забил на эту тему, потому что не мог понять.

Открыл учебник Яковлева.

У него, если сравнивать с Мякишевым, как бы пропущены подробности про векторы и сразу дан упрощенный итоговый ответ в случае совпадения оси Х с напряженностью.
У Мякишева написано просто: "проанализируем две формулы и увидим, что". У Яковлева конкретно показано, что хитрым способом мы выносим минус за скобку и получаем

. Мякишев, видимо считает, что его читатели достаточно умны для такого.
После этого получается, что ответ на мой вопрос "откуда появился минус?" очень прост - потому что направление оси Х совпадает с напряженностью и потому, что за точку с нулевой потенциальной энергией выбрана точка (0,0,0) (это если читать Яковлева).
А в учебнике за 10-11 у Мякишева за нулевую точку берётся именно начало координат (ведь мы же оперируем понятием радиус вектора) и получается то же самое.
У Мякишева в учебнике за 10 класс потенциальная энергия в однрд поле приводилась на примере поля между пластинами конденсатора, где одна пластина принималась за точку с нулевым потенциалом. По сути, как если бы эта пластина была в точке х=0. Это дурацкое упрощение въелось в память и давало диссонанс "как так, потенциальная энергия получается меньше нуля".
Просто больше нуля она будет в том случае, если Х будет меньше нуля. И тогда, если поле будет толкать +заряд вправо, то относительно (0,0,0) энергия этого заряда будет сначала больше нуля, потом уменьшаться, потом станет нулевой, потом станет отрицательной относительно именно конкретно (0,0,0).
Возвращаясь к векторной форме у Мякишева, теперь становится понятно, как и почему из

получилось

По сути, получается что если сориентировать поле параллельно плоскости ХОУ, то получится, что заряды находящиеся в областях 1 и 4 будут иметь отрицательную потенциальную энергию, т.к. угол между радиус-вектором и напряженностью будет меньше 90 градусов, тогда косинус будет больше нуля и всё это на минус даст отрицательную энергию.
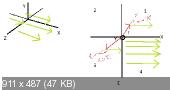
В областях 2 и 3 угол будет тупым, больше 90 градусов, это даст косинус меньше нуля и на минус всё это даст положительную энергию.
Иными словами, если мы так удачно выберем расположение осей относительно однородного поля, то пробные заряды будут обладать потенциальной энергией больше нуля "за" плоскостью ZOY и отрицательной "после" плоскости ZOY. Да и даже если не выберем, если использовать векторы - то вообще без разницы, как там располагаются оси координат относительно поля. Скалярное произведение во всём "поможет" найти правильное значение. Просто тогда граница "нулевого уровня" будет из себя представлять плоскость, перпендикулярную вектору напряженности и проходящую через начало координат.
Вроде всё понятно, но дальше снова завал.
Вопрос а что будет, если пробный заряд будет находиться НА плоскости ZOY ? Ведь тогда угол между ним и вектором напряженности в данной точке будет равен 90 градусам, что в итоге даст 0. Например, если координаты радиус вектора будут (0, 0, 4). Т.е. вектор лежит на оси OZ, в плоскости ZOY.



