Продолжим
фрактальную тему
О фракталах в Интернете написано не мало, но и не так много, как хотелось бы. Более того, не смотря на то, что о фрактальных кривых известно еще с начала прошлого столетия (треугольник Серпинского - 1915, кривая Леви - 1906, кривая Гильберта - 1891, ...), фракталы до сих пор остаются одной из самых малоизученных областей науки. Именно науки в целом, а не конкретно математики. Исследуя фракталы, можно узнать очень много о нашей Вселенной, ведь Вселенная - это фрактал. В качестве разминки для ума, попробуйте поискать самоподобие в окружающей вас действительности. Несколько самых очевидных примеров:




Вот, кстати, еще один пример. Почка человека похожа на эмбрион.
Эмбрионы разных животных:

...
Вообще, существует очень много способов (алгоритмов) построить фрактал. Об одном из таких алгоритмов впервые узнал в 2005 году. Простота этого алгоритма и, вместе с тем, разнообразие фракталов, которые можно нарисовать этим алгоритмом, сразу поразили мое воображение!
Рассмотрим этот алгоритм на примере кривой Леви.
Есть у нас две точки A1 и A2. Найдем такую точку A3, для которой угол A1 равен 45°, а угол A3 равен 90°.
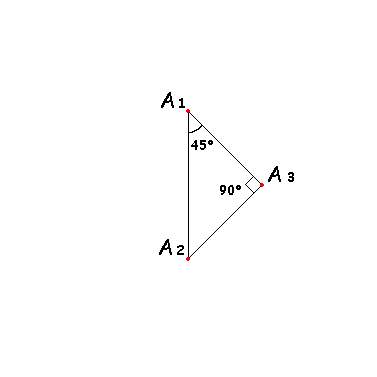
Проделаем ту же операцию для точек A1, A3 и A3, A2.
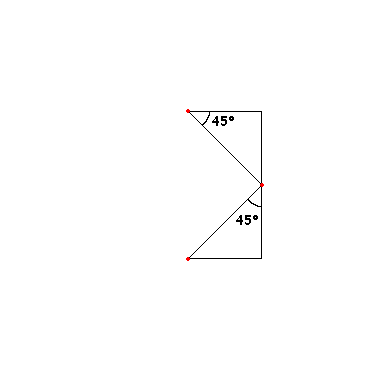
Следующая итерация:

Если продолжать эту операцию рекурсивно для каждой пары полученных точек, получим вот такую кривую:

Можно попробовать чередовать углы: 45° и -45°. Вторая итерация:
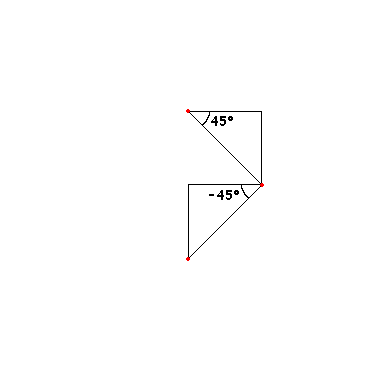
Третья:

14:
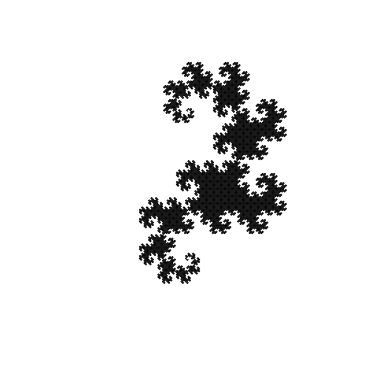
Получили другую известную фрактальную кривую — Дракон Хартера-Хейтуэя (придумана тремя умными дядьками из NASA).
Смотрите, как до неузнаваемости изменилась наша фрактальная кривая! В динамике (изменяем второй угол с шагом в 5°)
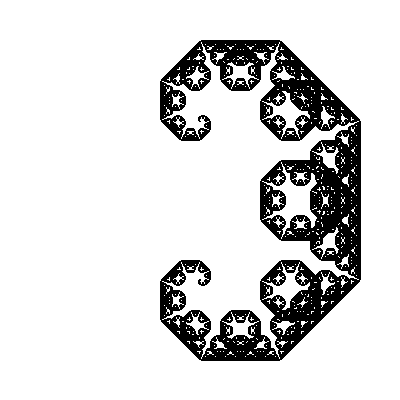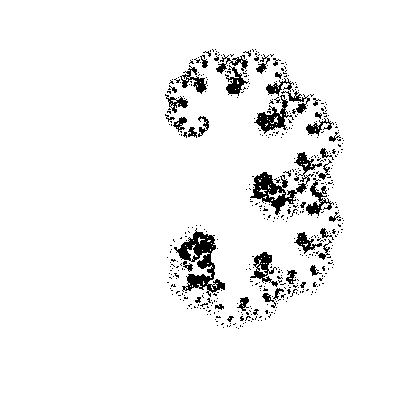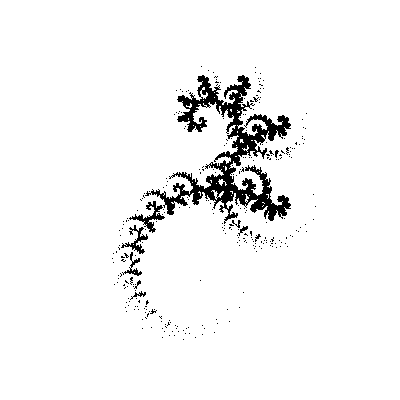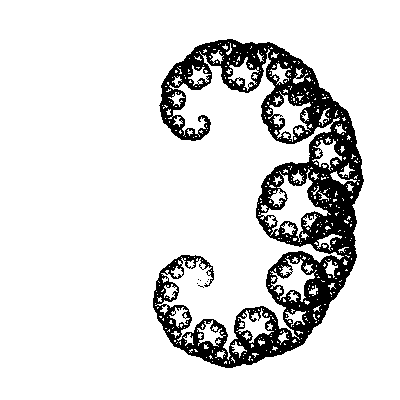
Я, признаться, немного удивлен, почему до сих пор никто не попробовал использовать этот алгоритм с другими углами (Скажем, [30°,-60°]. Или [30°,-30°,-60°,60°]). Во всяком случае, в Интернете не получается найти ничего похожего на те фракталы, которые нарисовал в 2005 году.
Несколько рандомных фракталов (точки не соединял линиями из эстетических соображений) с углами -45°/45° (кликабельно):





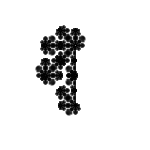







С углами -30°/30°/-60°/60°:











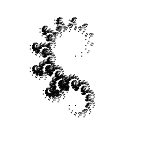













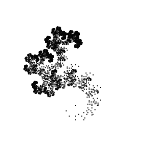


С углами -15°/15°/-30°/30°/-45°/45°/-60°/60°/-75/75°:

























Этим алгоритмом можно нарисовать внушительное количество фракталов. Например, если использовать только 8 углов (положительных и отрицательных из диапазона: 15°/30°/45°/60°/75°) - можно нарисовать 50 000 000 фракталов (если не считать симметричные фракталы). Согласитесь, вручную просмотреть все фракталы не представляется возможным. Поэтому нам поможет генетический алгоритм.
Генетический алгоритм - штука тоже очень простая и, вместе с тем, эффективная. Запишем углы как гены. Например, фрактал, нарисованный 8 углами, содержит 8 генов в генотипе. Создаем начальную популяцию из небольшого числа фракталов - гены в генотипах заполняем случайным образом. Далее, выбираем (вручную, сравнивая случайные пары фракталов) те фракталы, которые нам больше всего нравятся и запускаем эволюционный механизм. Не выбранные фракталы "вымирают", из выбранных создаем новую "популяцию": разбиваем популяцию выбранных фракталов на пары и для каждой пары формируем двух потомков. Берем ген первого или второго родителя (случайно) и записываем на соответствующую позицию в генотипе первого потомка (ген не выбранного родителя уходим второму потомку). Так для всех генов в генотипе. Наглядно-схематически:
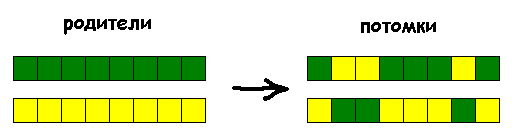
Заполнили новую популяцию родителями и потомками. Теперь некоторый процент особей в новой популяции мутирует (берем случайный ген и заменяем случайным значением) - тем самым разбавляем генофонд.
Вот так это безобразие выглядит:

Получаются очень интересные "особи":






Несколько "эмбрионов" на закуску:
 Подробное описание с исходниками: https://habrahabr.ru/post/328568/
Подробное описание с исходниками: https://habrahabr.ru/post/328568/
Исходники: https://github.com/xcont/fractalsВот тут можно поиграться с эволюцией "фрактальных монстров": http://fractal.xcont.com/


