Взаимно простые числа, числа Фибоначчи и фракталы.

[xcont]

Паттерн

В 2002 году придумал интересную штуку. 14 лет тогда было. Размышлял о фракталах и теории хаоса, а учиться не хотел. Учиться не хотел, а в школу ходить заставляли. Придумал способ убить время на скучных уроках по истории, географии и прочей гуманитарии. Попробую объяснить подробно. Все, что нам нужно - листок в клетку и карандашик. Если листка в клетку нет в наличии и карандашик тоже отсутствует - онлайн версия на JavaScript http://xcont.com/pattern.html

Алгоритм прост до неприличия. Собственно выглядит сие вот так:



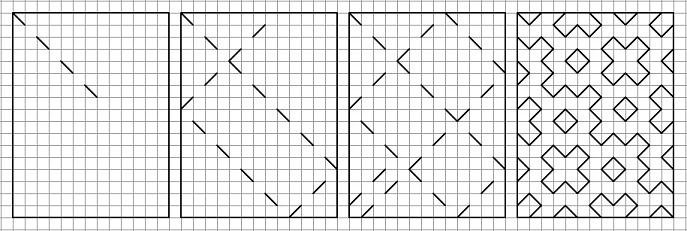
Выделяем прямоугольную область и пускаем из угла "квантовый луч" (так я его называл в 2002 году - сильно за терминологию не ругайте). Луч отражается от стенок и пропадает в другом углу.

Если соблюдаются определенные условия (об этом дальше) - получается фрактальный (об этом тоже дальше) узор-паттерн.
Если условия не соблюдаются (очевидный например - стороны прямоугольника равны) - узор не получается. Из менее очевидных напримеров - узор так-же не получается, если размеры сторон имеют общий делитель. Фактически, узоры получаются только если размеры обоих сторон - взаимно простые числа (не имеют общего делителя).

Наглядно (и кликабельно):



кстати, все сделано вручную, по пикселям в Paint

На картинке все числа от 1 до 30.

А теперь немного о Фибоначчи и фракталах.

Все узоры представляют из себя фракталы.

От чего зависит узор?

Цитата:

А потому, что нужно, чтобы разница тоже была простым числом (наиболее большим), его разница с числами тоже была простой и не маленькой, и т.д., тогда будет что-нибудь интересное.

Что наводит нас на мысль - а если попробовать числа Фибоначчи? Пацан сказал - пацан сделал.


Закрашивал в Paint самые большие замкнутые области.





233х144:






987х610 (скукожил в 5 раз):


233х144 и 987х610 - идентичны :)

Фракталы, как они есть.

Что еще можно из этого сделать

1. Попробовать не прямоугольную область, а скажем элипс.
2. Попробовать сделать в трех измерениях.
3. Обнаружить другие интересные зависимости между числами и рождаемым ими фракталом.

На хабре: http://habrahabr.ru/sandbox/68846/

P.S.

И немножко шизофрении 11-ти летней давности:

Цитата:

Тогда размышлял, о соотношениях хаоса и порядка, откуда в хаосе берется порядок, и в порядке - хаос. Так вот была тогда мысль, что когда все взорвалось (большой взрыв, в который я свято верил), был луч электромагнитной энергии который в начале бегал в маленьком пространстве (которое далее расширялось). Поскольку электромагнитные волны можно представить в виде квантов - этот луч не непрерывный. Там где мы видим пересечения электромагнитных волн - там появляется "материя" (http://ru.wikipedia.org/wiki/Рождение_пар) в виде фрактальных узорчиков. Так из хаоса рождается порядок.

(2) у пространства нет кванта расстояния - поэтому нет общих делителей. Всегда получается узор (то, что мы называем материей).
(1) вселенная расширяется непрерывно и плавно. Узорчик непрерывно (и тоже плавно) переходит из одного в другой - то, что мы называем движением материи.

Цитата:

Ну и еще выводы:
1. Вселенная не двухмерная, а трехмерная (а с точки зрения Общей Теории Относительности - четырехмерная).
2. Опять-же, с точки зрения ОТО - вселенная - не прямоугольная. Топологически, вселенную можно представить в виде тора.
Поэтому узорчики на порядок сложнее.

Идентичный паттерну 4х3:


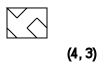
Кликабельно:


PS. PS. Касательно применения. Вчера вечером глядя на картиночки выводов наделал. Очевидных:
1. Два соседних числа Фибоначчи - взаимно простые.
2. Если два числа a1 и a2 (a2>a1) - взаимно простые, тогда взаимно простые так-же: a1 и (a2-a1)
3. Если два числа a1 и a2 (a2>a1) - взаимно простые, тогда взаимно простые так-же: a2 и (a2+a1)
4. Если в последовательности a(n)=a(n-1)+a(n-2) (следующее число - сумма двух предыдущих) есть два взаимно простых соседних числа, тогда в этой последовательности ВСЕ соседние числа - взаимно простые.
5. Ну и опять-же, если в такой последовательности одно число - простое, тогда ВСЕ соседние числа в этой последовательности - взаимно простые.
6. Два числа - взаимно простые, если в сумме дают простое число

А сколько еще можно выводов наделать?...

PS. PS. PS.

[Sonic86]

Жаль, во фракталах я не разбираюсь.

Могу только такое сказать: узоры выше (построенные на числах Фибоначчи) - это не фракталы. Т.е., я, конечно, понимаю, что определения у фрактала пока нет, но у приведенных узоров хаусдорфова размерность - целое число. Т.е. сравните с классическими фракталами и поймете.
Я поэтому буду говорить "узор".
Пока только один интересный вопрос вижу: определить, при каких соотношениях сторон построенные кривые будут замкнуты (или хотя бы - без концов).
И еще: можно ли узор продлить на всю плоскость? Всегда ли он периодический? Сколько получается типов узоров?

xcont в сообщении #756623 писал(а):

1. Попробовать не прямоугольную область, а скажем элипс.
2. Попробовать сделать в трех измерениях.
3. Обнаружить другие интересные зависимости между числами и рождаемым ими фракталом.

Можно попробовать брать не одну пунктирную линию, а 3, под углами в $\frac{2\pi}{3}$. Рисовать, конечно, будет сложнее.
Насчет кривых областей - как-то сложно. Проще существующие узоры конформно отображать в какие-нибудь кривые области. И, кстати, если отображения будут иметь особые точки, то в результате, наверное, получатся реальные фракталы.

Насчет выводов:

xcont в сообщении #756623 писал(а):

1. Два соседних числа Фибоначчи - взаимно простые.
2. Если два числа a1 и a2 (a2>a1) - взаимно простые, тогда взаимно простые так-же: a1 и (a2-a1)
3. Если два числа a1 и a2 (a2>a1) - взаимно простые, тогда взаимно простые так-же: a2 и (a2+a1)
4. Если в последовательности a(n)=a(n-1)+a(n-2) (следующее число - сумма двух предыдущих) есть два взаимно простых соседних числа, тогда в этой последовательности ВСЕ соседние числа - взаимно простые.
5. Ну и опять-же, если в такой последовательности одно число - простое, тогда ВСЕ соседние числа в этой последовательности - взаимно простые.

Это все очень просто. Верно, конечно.

xcont в сообщении #756623 писал(а):

6. Два числа - взаимно простые, если в сумме дают простое число

Если указать явно, что числа натуральные, то будет верно.

Можете книжек скачать про фракталам - удовлетворите свое любопытство.

И bot на соседнем форуме Вам правильно сказал: к физике это все отношения не имеет.

[xcont]

Цитата:

Мандельброт дал строгое математическое определение фрактала, как множества, хаусдорфова размерность которого, строго больше топологической размерности. Он однако так и не был удовлетворен этим определением, так как оно не включает в себя некоторые множества, рассматриваемые многими математиками, как фракталы.

-- 23.08.2013, 06:34 --

Я тут размерность насчитал в пределах 1.23 - 1.27

[Sonic86]

xcont в сообщении #756800 писал(а):

Я тут размерность насчитал в пределах 1.23 - 1.27

У какой фигуры? Фигура на последней картинке - не та, что на исходных картинках. Связь между ними есть, конечно, ее можно выписать, посмотреть на нее.

[xcont]

Sonic86, не могли бы вы рассказать, как считали хаусдорфову размерность?

[xcont]

-- 27.08.2013, 02:20 --

Часть фрактала, увеличенная в раз, подобна всему фракталу.

[Sonic86]

xcont в сообщении #758008 писал(а):

Sonic86, не могли бы вы рассказать, как считали хаусдорфову размерность?

Для прямоугольника в клетку размером $(F_{n+1},F_n)$ просто: линия состоит из конечного числа отрезков, размерность каждого - $1$, значит размерность всей ломаной - $1$ (или: кривая дифференцируема везде, кроме конечного числа точек). Тут тривиальный случай короче.

А вот последняя фигурка - уже реально фрактал. Его надо: описать построение (попробовать описать как бесконечное замощение (это опять узор), посмотреть, периодическое оно или нет), попробовать зажать в прямоугольник $[1;\varphi]$ и описать там итеративно (и тогда это уже фрактал). И тогда хаусдорфова размерность последнего мне неясна, конечно.

Ну и попробовать заменить числа Фибоначчи на другую последовательность пар чисел.

[xcont]

Sonic86 в сообщении #758216 писал(а):

попробовать зажать в прямоугольник $[1;\varphi]$ и описать там итеративно (и тогда это уже фрактал).

Использование чисел Фибоначчи - это как раз попытка наоборот, разжать его из прямоугольника $[1;\varphi]$. С числами Фибоначчи имеем отношение сторон - приближенное значение числа $\varphi$.
Если же одна из сторон - иррациональное число - тогда программно нереализуемо, поскольку не понятно, какие условия описать для выхода из цикла. В иррациональном прямоугольнике луч будет отражаться бесконечно.
"Итеративность" тут достигается приближением отношений сторон к числу $\varphi$, или же к прямоугольнику $[1;\varphi]$.

[warlock66613]

xcont в сообщении #758439 писал(а):

Если же одна из сторон - иррациональное число - тогда программно нереализуемо, поскольку не понятно, какие условия описать для выхода из цикла.

for(int i = 100000; --i >= 0; )

Число побольше поставить, но так чтобы отрабатывало не слишком долго, и всё.

[xcont]

warlock66613 в сообщении #758442 писал(а):

и всё.

А $\varphi$ на глаз отмерять?

-- 28.08.2013, 18:46 --

[Sonic86]

Вот такой вопрос: сколько существует типов узоров?
Можно ли вообще типы друг от друга отделить, или они переходят друг в друга? В общем, хочу описание всех узоров.

Пусть $p,q$ - стороны прямоугольника, $H(p,q)$ - узор, построенный на прямоугольнике со сторонами $p,q$. Считаем, что $p,q$ взаимно просты.
Вот квазитипы:
1. $H(F_{n+1},F_n)$
2. $H(136,127)$
3. $H(162,189)$
Типы должны обладать свойством: $H(p,q)\sim H(p,q\bmod p)$ (проверьте по рисункам). Правда, отсюда следует, что есть лишь один тип Но тогда сколько у него "естественных параметров"? Или это тоже бессмысленный вопрос и параметров всего 2?

Ага, я понял: что-то зависит от начальных условий.
Пусть $a_1=1, a_2=k, a_{n+1}=ba_n+a_{n-1}$, причем $k$ фиксировано, а $b$ - вообще любое. Тогда $H(a_{n+1},a_n)$ имеют явно один и тот же квазитип для любого $b$, а $b$ естественным образом характеризует получаемый узор. Можно этим узором замостить всю плоскость.
Может типы узоров нужно отличать по замощению ими всей плоскости?

[warlock66613]

xcont в сообщении #758447 писал(а):

А $\varphi$ на глаз отмерять?

В смысле на глаз? Вы имеете в виду, что оно должно быть иррациональным, а в компе все числа рациональные? Так это не проблема. Можно взять рациональное, но чтобы побольше знаков было после запятой. А можно сделать настоящее иррациональное число, используя паттерн "монада".

[xcont]

Sonic86 в сообщении #758517 писал(а):

$H(p,q)\sim H(p,q\bmod p)$

Запись не понятна. Я не математик. Можете объяснить, если вас это не затруднит?

[arseniiv]

xcont, ваши фигуры, конечно, самоподобны, но «не до конца», так что это не фракталы. Итерация кривой дракона, которая у вас на аватаре, к ним ближе. (Она тоже не фрактал.)

(Оффтоп)

xcont в сообщении #756623 писал(а):

кстати, все сделано вручную, по пикселям в Paint

Это ж только в минус, лучше бы не упоминали об этом вообще.

-- Ср авг 28, 2013 23:27:07 --

xcont в сообщении #758533 писал(а):

Запись не понятна. Я не математик. Можете объяснить, если вас это не затруднит?

$\sim$ — эквивалентность, $a \bmod b$ — остаток от деления $a$ на $b$.

[xcont]

"Типов" как раз больше, чем хотелось бы. Если использовать не пунктирный луч, а плавно меняющий интенсивность, получим совсем другие "узоры":















К тому-же, можно попробовать использовать длину луча не $\sqrt{2}$, а скажем, число $\pi$

(Оффтоп)

arseniiv в сообщении #758534 писал(а):

xcont в сообщении #756623 писал(а):

кстати, все сделано вручную, по пикселям в Paint

Это ж только в минус, лучше бы не упоминали об этом вообще.

Я дзен-буддист))) Столько дзена наотлавливал, пока этот квадратик сделал - любой дзен-буддист обзавидуется)))