Как у вас вообще энергия основного состояния в формулу попадает? Давайте пишите формулы, не надо словами.
Вот мой расчет (пояснения на английском). Получилась интереснейшая вещь (см. ниже).
Let us assume a gas has such a temperature that the translational and rotational degrees of freedom are "fully" excited but vibrational degrees are not (for hydrogen this situation takes place at room temperatures and higher). For this case according to the Einstein's theory of specific heat the expression for the internal energy of the diatomic gas can be written as follows:
![$U(T) =\left[\frac{5}{2} +\left( \frac{\hbar\omega}{kT}\right)\frac{1}{\exp(\hbar\omega /kT)-1} \right] \nu RT$ $U(T) =\left[\frac{5}{2} +\left( \frac{\hbar\omega}{kT}\right)\frac{1}{\exp(\hbar\omega /kT)-1} \right] \nu RT$](https://dxdy-03.korotkov.co.uk/f/6/a/c/6acdd58761c7362238888ec0deccadb582.png)
, (1)
where

is the amount of substance,

is the gas constant,

is the absolute temperature;
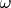
is the molecular vibrational frequency (for hydrogen
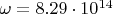
~
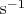
);
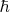
and

are respectively the reduced Planck and Boltzmann constants. If we introduce the Einstein temperature
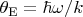
(for hydrogen
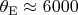
~K) and put
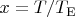
then the the molar heat capacity at constant volume
![$c_{\mu V}(T) =\frac{dU}{\nu dT} =\left[\frac{5}{2} +\frac{\exp(1/x)}{x^2(\exp(1 /x)-1)^2} \right]R$ $c_{\mu V}(T) =\frac{dU}{\nu dT} =\left[\frac{5}{2} +\frac{\exp(1/x)}{x^2(\exp(1 /x)-1)^2} \right]R$](https://dxdy-01.korotkov.co.uk/f/8/e/6/8e6ed415f32998ac438f6b481f9c8a0d82.png)
(2)
Let us write the first law of thermodynamics for the adiabatic process (
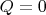
, where

is the amount of heat) in the differential form:
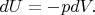
But
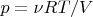
and using the formula (2) we get:
![$\left[\frac{5}{2} +\frac{\exp(1/x)}{x^2(\exp(1 /x)-1)^2} \right] \frac{dx}{x}=-\frac{dy}{y}. $ $\left[\frac{5}{2} +\frac{\exp(1/x)}{x^2(\exp(1 /x)-1)^2} \right] \frac{dx}{x}=-\frac{dy}{y}. $](https://dxdy-01.korotkov.co.uk/f/0/6/a/06a1651f5d94a2bdea921bfebc9c041c82.png)
Here we introduce the dimensionless volume
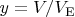
, where
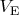
is the gas volume at

. Integrating both sides of this equality we obtain:

where

is the integration constant. Using the described above initial condition we finally derive:
![$\frac{\exp\left[ \frac{1}{x(1-\exp(-1/x))} \right] }{\exp(1 /x)-1}yx^{5/2}=C\approx 2.83.$ $\frac{\exp\left[ \frac{1}{x(1-\exp(-1/x))} \right] }{\exp(1 /x)-1}yx^{5/2}=C\approx 2.83.$](https://dxdy-01.korotkov.co.uk/f/0/4/a/04acf988d9e78e3ed2cfcb99429d71af82.png)
(3)
It follows from the equations (2), (3) that it is incorrect to simply replace
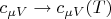
in the adiabatic index

(the heat capacity ratio) to adequately describe the equation of the adiabatic process and in fact the situation is more complicated. If
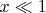
from the relation (3) we have:
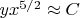
. In the opposite case of very high temperatures (
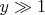
) the equation of the adiabatic process is
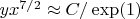
.



