Доказательство для произвольного топологического пространства

. Чтобы была аналогия с обсуждавшимися доказательствами, я буду предполагать, что для каждой точки

выбрана некоторая база топологии
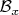
в точке

, элементы которой называются окрестностями точки

(в случае метрического пространствоа в качестве такой базы обычно берётся множество открытых шаров с центром в данной точке или часть этого множества, содержащая шары сколь угодно малого радиуса).
Пусть

- некоторое множество,

- его граница,

- точка прикосновения множества

. Берём любую окрестность

точки

. Так как

- точка прикосновения множества

, то найдётся точка

. Так как

- база топологии пространства

в точке

, найдётся окрестность

, удовлетворяющая условию

. Поскольку

, выполняются условия

и

. Тем более

и

. Поэтому

. Таким образом, множество

содержит все свои точки прикосновения и, следовательно, замкнуто.



