И клетку с ненулевым собственным числом?
Ну располовиньте в предыдущем примере первые три строчки.
Реализую эту идею для получения клетки

,

.
Матрица

соответствует случайному блужданию на отрезке с вероятностью

остаться на месте и

сделать шаг вправо, крайнее правое состояние поглощающее. Она блочно-верхнетреугольная, имеет характеристический

и жорданов базис

Таким образом, построена стохастическая матрица, жорданова форма которой имеет клетку произвольного размера с неотрицательным числом.
Здесь остаются вопросы: а) о возможности получения клетки с отрицательным числом


; (не смог построить неотрицательную матрицу с

)
б) о возможности построения матрицы

эргодической цепи
(т.е.

),

),
подобная которой содержит

,

.
-- 29.05.2017, 18:43 --Optimizator, запишите условия стохастичности по строкам и столбцам, потом посмотрите, чему они соответствует в векторном виде.
Пишу:

,
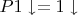
, но продолжения идеи (для доказательства положительности матрицы) не вижу...