Задача 7*.
Из всякой последовательности можно выделить монотонную подпоследовательность.
Доказательство.
...
в) если

, то помещаем

в обе подпоследовательности так, чтобы их монотонность сохранилась
Кажется тут у меня полная фигня, так нельзя.
Я придумал новый алгоритм (на самом деле доработал старый), надеюсь без фигни на этот раз.
Пусть

-- произвольная последовательность. Начнем с формирования двух различных монотонных подпоследовательностей -- неубывающей и невозрастающей, поместив в каждую

в качестве их первого члена. Далее последовательно перебираем все остальные

, начиная с

, и сравниваем их с последними членами во всех формируемых монотонных подпоследовательностях. Если

не меньше последнего члена в формируемой неубывающей подпоследовательности, добавляем его туда. Аналогично, добавляем

в невозрастающую подпоследовательность, если он не больше последнего члена в ней. Если

не был добавлен ни в одну из формируемых подпоследовательностей (т.е.

оказался больше всех последних членов невозрастающих подпоследовательностей и меньше всех последних членов неубывающих подпоследовательностей), то в дополнение к предыдущим начинаем формировать две новые монотонные подпоследовательности - невозрастающую и неубывающую, и помещаем в них

в качестве первого члена.
Пусть

- число начатых формироваться монотонных подпоследовательностей за время работы алгоритма. Каждые 2 шага алгоритма могут начинать формироваться 2 новые монотонные подпоследовательности. Каждый

присутствуют как минимум в одной монотонной "подпоследовательности".
На выходе алгоритма возможны следующие результаты:
а)

конечно, следовательно какая-то из сформированных монотонных подпоследовательностей счетна, и мы получили что хотели.
б)

счетно, и все начатые формироваться монотонные "подпоследовательности" конечны. Тогда составим из их последних членов 2 новые монотонные подпоследовательности. Пусть

-- последовательности последних членов сформированных невозрастающих и неубывающих "подпоследовательностей" соответственно, идущие по порядку начала формирования этих "подпоследовательностей". Тогда

,

для
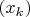
, и

,

для

. Таким образом,

-- возрастающая и убывающая подпоследовательности

соответственно.