К упражнениям о преобразованиях Лоренца добавка: надо убедиться (не обязательно на форуме), что
.
преобразуются как левый и правый 2-компонентные спиноры.
. Пусть
преобразуется как правый спинор. Пусть
но зато меняет знак при комплексном сопряжении. Поэтому протаскивание
. Нам потребуется преобразование Фурье (указанные ниже свойства следует проверить, запомнить выбор множителей, выбор знаков в показателях. Фурье-компоненту
(или для совокупности функций - компонент спинора) обозначаем ради краткости той же буквой, хотя это разные функции. Следует отличать
хотя это не указывается явно).
Переходим к знакомству с фейнмановским пропагатором вейлевского фермиона. План видится такой. Сначала убедимся, что с пропагатором связаны 1-частичные амплитуды перехода между источником и приёмником равноправно для частицы и для античастицы. Пример вейлевского фермиона хорош простотой: такой фермион хотя и обладает спином, но не обладает спиновой "степенью свободы" - спин левой частицы всегда направлен против её импульса, а её античастица - всегда правая, со спином вдоль импульса. В дальнейшем сравнение с этим примером поможет понять более сложный пример: дираковский фермион с массой; у него есть спиновая степень свободы - спин может иметь любое направление относительно импульса.
Пусть заданы два спинорных поля:

и

оба правые в смысле закона преобразования при бустах. Слово "заданы" означает, что мы не считаем их решениями уравнений движения; они произвольные, и поэтому в фурье-разложении

и

по плоским волнам отличны от нуля амплитуды не только правых спиноров (в смысле со спином вдоль импульса) но и левых. Правые и левые базисные спиноры будем обозначать как

и

Частота

у плоских волн произвольно заданных полей принимает всевозможные положительные и отрицательные значения, а не только

Назовём

и

источниками; ниже выяснится, что тот источник, который включается во времени раньше, служит источником частиц, а который позже - приёмником.
Аналогия
в классической механике: осциллятор в присутствии заданной внешней силы

Уравнение движения осциллятора

есть

Пусть

действует (т. е. может быть не равна нулю) только на конечном интервале времени

и пусть в её фурье-разложении есть составляющая с частотой свободных колебаний осциллятора

и пусть до начального момента времени

осциллятор покоился. Тогда

служит источником колебаний осциллятора, т. е. источник передаёт осциллятору энергию: после выключения силы, при

осциллятор будет совершать колебание с собственной частотой

амплитуда его пропорциональна фурье-амплитуде силы

на этой частоте.
Если до включения

осциллятор уже совершал колебание, то сила

может его затормозить: после её выключения амплитуда колебаний станет меньше или даже осциллятор окажется покоящимся. В этих случаях источник является приёмником энергии от осциллятора.
Ещё вариант: если

состоит из двух неперекрывающихся во времени слагаемых,

и фурье-амплитуды слагаемых на собственной частоте осциллятора

отличны от нуля, но в сумме взаимно уничтожаются, то осциллятор, покоящийся до включения первой части силы, останется покоящимся и после выключения последней части, а в промежутке времени между окончанием первой части и началом второй он будет совершать свободное колебание с частотой

Здесь происходит передача энергии от более раннего источника

к позднему

Аналогичные задачи есть и
в квантовой механике:
Покою классического осциллятора отвечает "основное состояние" квантового осциллятора" (а в КТП - "вакуум"). Если в классической задаче фурье-амплитуда источника на частоте

мала, так что отдаваемая или получаемая им энергия колебаний мала по сравнению с

то в КМ это проявится как малость
вероятности того, что источник изменит состояние осциллятора. Такой источник будем называть
слабым.
В классической теории поля:
Вместо колебаний одного механического осциллятора

рассматриваются "осцилляторы поля" - волны поля в пространстве-времени; поэтому вместо одной собственной частоты

в задаче появляется множество собственных частот

"пронумерованных" волновым вектором
 В КТП
В КТП:
Кванты энергии

и импульса

"осцилляторов поля" трактуются как частицы. Волны остаются только в роли инструмента для расчётов. Различные состояния "мира" описываются не картиной волн в нём, а количеством всевозможных частиц (и античастиц).
В задаче механики об осцилляторе мы можем не вникать в устройство источника силы

Аналогично и в КТП: источник

лишь феноменологически описывает совокупность физических условий, которые в данной области пространства-времени (где

может быть не равной нулю) обеспечивают возможность рождения или поглощения частиц. Поскольку функция

задана, то не учитывается влияние актов рождения и поглощения частиц на "состояние самого источника".
Спинорные источники

и

будем считать слабыми и действующими на конечных неперекрывающихся интервалах времени. Сначала рассмотрим случай, в котором пространственно-временная область с ненулевым

расположена раньше (т. е. в и/или на конусе прошлого) области, где задан ненулевой

Пусть квантовое состояние "мира" в нашей модельной задаче в далёком прошлом является вакуумным (ноль частиц), обозначим его как

На любой пространственно-подобной поверхности в будущем после окончания действия слабого источника

но до того, как начнут действовать другие источники, состояние "мира" может остаться вакуумным (с вероятностью, близкой к

либо оно окажется 1-частичным (c вероятностью, малой в меру слабости источника), либо двух- и более частичным (этими вероятностями пренебрежём).
Амплитуды вероятностей это матричные элементы оператора эволюции. Интересуясь в первую очередь амплитудами перехода из

в то или иное 1-частичное состояние, возбуждённое источником

и учитывая, что 1-частичные состояния могут различаться импульсом частицы, обозначим эти амплитуды так:

Слабый источник

действующий после выключения

с вероятностью, близкой к

не изменит состояния "мира", либо с малой вероятностью добавит ещё одну частицу, либо поглотит имеющуюся. В последнем случае состояние в будущем опять становится вакуумным; амплитуду вероятности такого перехода обозначим как

Амплитудами прочих переходов (т. е. многочастичных) пренебрежём.
С учётом всего этого 1-частичный вклад в амплитуду перехода

из начального вакуума в конечный вакуум при наличии источников

и

указанным образом упорядоченных во времени, должен иметь вид суммы вкладов, отвечающих различным импульсам частицы:

Связь этих амплитуд с функциями

и

можно предвидеть из соображений об однородности пространства и времени, варьируя положение источников. Сместим

на любое время

в прошлое, т. е. заменим

на

Тогда эволюция состояния, рождённого источником

к прежней гиперповерхности будущего займёт добавочное время

и оно привнесёт в матричный элемент оператора эволюции добавочный фазовый множитель

где

- энергия состояния. Для 1-частичного состояния:

Аналогично, сдвиг источника

на любой вектор

т. е. замена аргумента

на

должна дать фазовый множитель

где

- импульс состояния. Для 1-частичного состояния

Именно такие фазовые множители выпускает фурье-амплитуда функции источника с аргументами

и

, и, значит, амплитуда перехода

связана с данной фурье-амплитудой:

Матричные элементы оператора эволюции подчинены условию унитарности. Можно показать, что оно ведёт к определённому соотношению между амплитудами перехода с рождением и с поглощением частицы заданным слабым источником:

Поглощать частицу у нас будет источник

так что:

Теперь найдём в общем виде спинорное поле

являющееся решением уравнения движения со спинорным источником


Подставив сюда фурье-разложения по плоским волнам для

и

получим уравнение для спинорной фурье-амплитуды

(пишу в кратком виде, сделать выкладки в подробной записи - упражнение):

Умножив обе стороны на

и учитывая, что

получим:

Чтобы получить обратным фурье-преобразованием искомое поле

надо в интеграле по

задать правило обхода полюсов

В КТП работает правило Фейнмана: к собственным частотам поля (у нас это

добавляется бесконечно малая отрицательная мнимая часть

Изменённая так функция

называется скалярным безмассовым фейнмановским пропагатором

в 4-импульсном представлении:

Матрицу

можно назвать спинорным пропагатором в 4-импульсном представлении; так что:

В координатном представлении:

Вычислим это поле

после окончания работы источника

т. е. при

где

- значения времени в области действия источника

Интегрирование по

выполним контурным методом. Чтобы выбрать контур, заметим, что в интеграле

пределы можно заменить начальным и конечным значениями

между которыми действует

так как всюду вне этого интервала времени

и вклада в интеграл нет. Подставив эту формулу в интеграл по

для

увидим, что там имеется экспонента с показателем

Поскольку

она убывает при устремлении

к

Это означает, что путь интегрирования вдоль вещественных значений

от

до

можно замкнуть полуокружностью бесконечного радиуса в нижней полуплоскости комплексной пременной
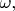
и такая полуокружность не даст вклада в результат. Результат есть

в полюсе подынтегрального выражения при

попавшем внутрь этого замкнутого контура:

Заметим, что

есть спинорный проектор, выделяющий из любого спинора левую составляющую. Таким образом:

Видно, что роль пропагатора

свелась к "частотному и спинорному проецированию": для левого спинорного поля

этот пропагатор выделил из фурье-составляющих

источника

только левые и только положительно-частотные моды с частотами колебаний свободного поля

Теперь вычислим результат взаимодействия этого левого спинорного поля с правым спинорным источником

который у нас работает позже, чем

и поэтому может выполнять роль приёмника частиц. В локальной теории поля взаимодействие полей описывается произведением полей в одной и той же точке

пространства-времени (у нас это будет лоренц-инвариантная свёртка

и затем по

выполняется интегрирование. Чтобы получить вклад в амплитуду перехода "вакуум-вакуум" со всеми необходимыми множителями, интеграл следует домножить на фазовый множитель

(это можно показать подробным рассмотрением понятия "вакуумная амплитуда" - отдельная очень большая тема однако :) Итак, вычисляем, меняя по ходу дела порядок интегрирований по

и по


Видно, что здесь появляется фурье-амплитуда источника

(значком Т обозначим транспонирование):

так что:

Это выражение должно представлять

Чтобы придать ему такую форму, будем считать теперь, что поля рассматриваются в произвольно большом, но конечном нормировочном объёме

с условиями периодичности; при этом, как известно, волновой вектор дискретен, а переход от интегрирования к суммированию формально сводится к замене

на

Базисные спиноры

и

собственные с собственным значением

соответственно для проекторов

и

взаимно ортогональны:

Но мы их ещё не нормировали. Учитывая, что энергия или частота

как и плотность

, преобразуется подобно временн
ой компоненте 4-вектора, выберем следующие сохраняющиеся при лоренц-преобразованиях условия нормировки:

Числовые коэффициенты разложения по этим базисным спинорам обозначим так: для источника

буквами

для

буквами

для

буквами

для

буквами

причём выделим в каждом из них множитель

Следуя этой схеме, запишем сначала разложение по базисным спинорам для


Тогда (поскольку левый проектор вычёркивает слагаемое с правым спинором и не изменяет слагаемое с левым спинором):

Этот спинор теперь надо свернуть с

Учитывая ортогональность и нормировку базисных спиноров, получим:

Это выражение входит под знак суммы

так что окончательно можем записать одночастичный вклад в вакуумную амплитуду в виде:

Отсюда видны определения 1-частичных (но пока ещё не античастичных) амплитуд перехода через фурье-компоненты слабых спинорных источников:


Теперь повторим аналогичные вычисления, начав с той части решения

которая "распространяется назад во времени" - в область пространства-времени, предшествующую началу работы источника

При

найденное выше решение уравнения движения

определяется вычетом в полюсе пропагатора в верхней полуплоскости комплексной частоты и поэтому содержит отрицательно-частотные волны. Результат

можно переписать иначе, заменяя переменную интегрирования

на


и учитывая равенство


Тогда результат взаимодействия этого спинорного поля с источником

который на этот раз пусть работает раньше, чем

(т. е. это другой источник

и его следовало бы обозначить другой буквой, но для сравнения с предыдущим рассмотрением оставим прежнее обозначение), есть:

Вставим перед

единичную матрицу

и учтём, что матрица

вещественная и антисимметричная

и что

Получаем:

Разложим присутствующие здесь спиноры

и

по базисным спинорам

и




Заменив, как и выше, интегрирование

суммированием

имеем:

Этот результат интерпретируется как вклад в амплитуду перехода "вакуум-вакуум", в котором источник

действующий первым во времени, испускает
правую античастицу, а источник

действующий позднее, её поглощает. Обозначив наличие одной античастицы чертой над единицей, это утверждение можно записать так:

Равноправность частиц и античастиц выявляется, если определения 1-
античастичных амплитуд перехода через фурье-компоненты слабых спинорных источников ввести по той же самой схеме, что и для амплитуд с частицами; при этом, как видно, способность источников

и

создавать и поглощать античастицу описывается фурье-компонентами комплексно сопряжённых величин,

и



Тут всплывает нюанс. Расчёт

дал нам

Если переписать это с множителями

в соответствии с указанным выше определением амплитуд, то возникает минус перед суммой:

И очерёдность сомножителей под знаком суммы получилась обратной к ожидавшейся.
Всё это исправляется, если принять, что числовые амплитуды спиноров

и

это не обычные числа, а грассмановы, т.е. антикоммутирующие переменные. (Обоснование и обсуждение "как с этим жить" - отдельный сюжет. Антикоммутативность спинорных полей в "методе источников" ведёт в итоге к ферми-статистике спинорных частиц и античастиц, что и позволяет говорить о них как о фермионах. В методе вторичного квантования (метод полевых операторов) вместо грассмановых амплитуд вводятся, в случае фермионов, антикоммутирующие операторы рождения и уничтожения. Метод полевых операторов, наверное, проще для расчётов, чем метод источников; последний же, имхо, позволил нам нагляднее "въехать" в вакуумную амплитуду и пропагаторы).
Тогда:

и тогда для одно-античастичного вклада в "амплитуду перехода вакуум-вакуум в присутствии источников" получается понятная на вид формула - совершенно аналогичная одночастичному вкладу:

Резюмируя, полезно отметить, что решение

уравнения движения с источником

можно записать в кратком виде:

где

есть фейнмановский спинорный безмассовый пропагатор

в координатном представлении.
Тогда рассмотренный выше вклад

в амплитуду перехода "вакууум-вакуум"

возникающий за счёт распространения частицы или античастицы между источниками

принимает вид:

Если

действует позже, чем

это выражение описывает распространение частицы от

к

и сводится к

Если

действует раньше, чем

это выражение описывает распространение античастицы от

к

и сводится к

Если

и

разделены пространственно-подобным интервалом, то понятия "раньше, позже" для них теряют лоренц-инвариантный смысл, и рассматриваемое выражение не сводится к амплитудам перехода реальной (т. е. с энергией

) частицы или античастицы. В этом случае можно сказать, что пропагатор

описывает распространение виртуальной частицы или античастицы.



