Отрицательные числа в школе не проходили?
Похоже, что именно в этом всё дело
 Pereyaslavl
Pereyaslavl Попробуйте ещё раз вникнуть, спокойно и вдумчиво во всё Вам сказанное. Вдумайтесь в задачку о двух шарах на чётком языке формул векторной алгебры:
Пусть

обозначает вектор импульса, направленный туда, куда летит до столкновения лёгкий шар, скажем направо, а его величина (т.е. модуль вектора) пусть равна одной единице импульса:

Пусть до столкновения ваш лёгкий шар летит направо с импульсом в две единицы; тогда его импульс в векторном виде есть

Пусть ваш тяжёлый шар до столкновения покоится; тогда его импульс есть равный нулю вектор:

Значит, до столкновения суммарный вектор импульса двух шаров есть:

Допустим, как Вы и говорите, после лобового столкновения ваш легкий шар отскочил от тяжёлого налево, и величина его импульса после столкновения (т.е. модуль его вектора импульса после столкновения) равна

Так вот: поскольку направление его импульса поменялось на противоположное, то вектор импульса лёгкого шара после столкновения есть

Обратите внимание на минус; вот он как раз означает, что направление импульса поменялось на противоположное.
Рассуждаем дальше. Пусть
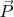
означает вектор импульса тяжёлого шара после столкновения (его мы должны найти). Тогда суммарный вектор импульса двух шаров после столкновения есть:

Как того требует закон сохранения импульса, приравняем суммарный вектор импульса двух шаров после столкновения к суммарному вектору импульса этих шаров до столкновения:

Получилось простенькое уравнение для вектора

Любой человек, знакомый с алгеброй, и если он не троль, элементарно решит это уравнение:

Отсюда совершенно очевидно и потому не удивительно, что

(Удивляться может только тот, кого удивляет решение элементарного уравнения

, т.е. человек, не понимающий отрицательных чисел. Да, такая беда бывает с невнимательными школьниками...)



