"Сложением" в математике обычно называют операцию какой-то абелевой группы.
Это всего лишь неформальная традиция. И нестрогая.
А участвующие в преобразовании Лоренца две скорости всё-таки имеют принципиально разную природу и относятся к различным векторным пространствам.
Можно сложить и две скорости одной природы из одного векторного пространства. Типичная постановка задачи:
ИСО  имеет скорость
имеет скорость  относительно ИСО
относительно ИСО  (то есть, получается из неё бустом на эту скорость), ИСО
(то есть, получается из неё бустом на эту скорость), ИСО  имеет скорость
имеет скорость  относительно ИСО
относительно ИСО 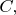 найти скорость
найти скорость  ИСО
ИСО  относительно ИСО
относительно ИСО 
Но верно замечание, что операция неабелева, по крайней мере в 2- и 3-мерном пространстве. (Кроме того, там бусты незамкнуты, и последовательность бустов даёт ещё и вращение.)
В физике словом "скорость" обозначают не только вектор скорости относительно некоторой системы отсчёта, но и, в более широком смысле, так называют любую производную некоторой величины по времени.
А в математике - и не только по времени. Ср. "скорость возрастания графика".
Но для скоростей как для векторов уже определена операция, которую называют сложением.
Э нет. Вот её приходится "разопределить". В частности, в СТО
скорость - не вектор.
Потом, это «сложение» разве не оказывается неассоциативным?
Ассоциативным, но некоммутативным. Это сложение в группе Ли




