Доброго дня!
Имеется недеформируемый шар радиусом

, который может катиться без проскальзывания по плоскости

. На поверхности шара есть выделенная точка. Для определенности будем полагать, что эта точка находится на расстоянии

от плоскости. Вопрос в том, может ли эта точка коснуться плоскости в любой наперед заданной её точке (допустим, это точка Б)? И если может, то какова кратчайшая траектория проекции центра шара на плоскость до момента касания?
Насколько я понимаю, вопрос о том, достижима ли любая точка плоскости решается положительно. За два перемещения мы сможем достигнуть любой точки в радиусе

от первоначального положения точки касания шара. Вот для примера путь достижения точки Б:
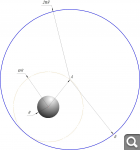
А как быть с теми точками, что находятся на расстоянии от первоначальной точки касания дальше, чем

? Я понимаю, что переместив шар в новую точку касания, мы тем самым сдвигаем и эту"окружность двукратного перемещения". Но вот со строгим соображениями не могу пока понять.
И, кроме того, не знаю, что именно делать с кратчайшей траекторией. Понятно, что ломаные наверное могут замениться на некие кривые. Но как тут подступиться - не понимаю.



