-Признателен всем тем участникам дискуссии, которые смотрят на поставленный вопрос с точки зрения: "все не так просто"(независимо от их аргументации): вы интуитивно правильно понимаете квантовую механику.

Однако, все же, вся дискуссия по этому вопросу - с одной стороны, и , с другой стороны, большая методическая методическая важность правильного понимания этой задачи, как яркого примера применения фундаментальных квантовомеханических концепций - побудили меня написать ниже подробный "педагогический" разбор всего, что происходит в такой системе, что означает идеология теории возмущений в данном случае, почему так важно эту идеологию использовать в данном случае и почему приведенное автором задачи pvp выражение - в принципе не может быть "точным решением" этой квантовомеханической задачи.
-Итак,
"Краткая лекция об особенностях квантовой динамики системы под действием зависящего от времени скачкообразного изменения ее гамильтониана."
Автор задачи, pvp, стал жертвой странного заблуждения или непонимания самых фундаментальных основ квантовой механики, поскольку задача, которую он формулирует, является абсолютно стандартной для квантовой механики и решается только приближенно, методом теории возмущений (см. напр. разделы: "Возмущения, зависящие от времени ", "Переходы под влиянием возмущения, действующего в течение конечного времени", "Соотношение неопределенностей для энергии" в т.3 Ландау-Лифшица , или, аналогичные разделы в любом другом курсе квантовой механики, можно напр. посмотреть вывод формулы для Fermi golden rule Sudden approximation в курсе Berkeley). Применительно к данной задачке с кусочно-постоянной функцией

, возмущением зависящим от времени является следующая часть гамильтониана:

, где функция:

- кусочно-постоянна и испытывает скачок в момент времени:

. Соответственно этому, условие , при котором приближенное решение задачи вообще существует, будет следующим:

(1)
, неравенство (1) нужно понимать в смысле собственных значений соответствующих операторов. Или, учитывая определение кусочно-постоянной функции

, условие (1) можно записать просто в виде ограничения на "высоту"

скачка функции

:

(2)
Если же условия (1, 2) применения теории возмущений - не выполняются, то можно математически строго показать, что, определяющие в этом случае эволюцию системы, высшие порядки в разложении Дайсона для точного оператора эволюции системы

будут полностью неопределенными из-за больших вкладов во временные интегралы от интервалов неопределенности гамильтониана системы "в момент" его скачкообразного изменения.
Для этого можно заметить, во-первых , что время - непрерывная, а не дискретная переменная, следовательно, правильно говорить не о точках, а об
интервалах определения функции

. Далее, очевидно, что функция

- не определена в малой

-окрестности (

) точки

, где

и, соответственно, значение

- в любой точке внутри интервала

- не определено, т.е. функция

там не дифференцируема. А это автоматически означает, что в каждом интеграле по

от 0 до

обязательно будет неопределенный вклад , пропорциональный

. И если в низших порядках разложения Дайсона для

вполне можно пренебречь вкладом этих неопределенностей , т.к. он порядка

по отношению к вкладу в интеграл от всего интервала

, то в высших порядках , когда

, какой бы большой порядок

мы не взяли , для него всегда найдется свой

, такой что, при

(

) отношение

вклада интервала неопределенности

по отношению к вкладу в этот

-ый порядок от всех временных интервалов

- будет стремиться уже не к

, а к

. Тогда если возмущение

будет достаточно велико , то вклад всех высших порядков в разложение Дайсона будет определяющим и, соответственно из-за полной неопределенности этих высших порядков , полностью неопределенным станет и весь точный оператор эволюции системы

, а значит , точное решение поставленной задачи в этом случае в виде какого-то точного оператора эволюции - также будет не определено. Вот, собственно, поэтому все подобные задачи решаются только в теории возмущений по малому параметру (1,2).
Иными словами, можно сказать, что время , в течение которого в системе может произойти скачок ее гамильтониана - это всегда некий временной интервал (на практике, разумеется, всегда конечный, в силу конечности скорости передачи сигнала , т.е. скорости света, а также конечной скорости работы всех "макроскопических" переключателей и пр. обеспечивающих этот скачок). Но это означает, что абсолютно во всех случаях, всегда существует какой-то отрезок временной эволюции квантовой системы, на котором ее гамильтониан существенно и резко (т.е. неадиабатически) меняется. Очевидно, что теоретический аппарат квантовой механики не в состоянии описать временную эволюцию квантовой системы на этом этапе. Ведь конкретный характер такой временной эволюции попросту неизвестен и не может быть описан динамически в рамках квантовой механики, точно так же, как в ней принципиально не может быть описан коллапс волновой функции в результате любого проективного (т.е. осуществленного макроскопическим "прибором") измерения квантовой системы, или например, "детали" квантовых переходов электрона в атоме. Во всех этих случаях, все что делает квантовая механика - она констатирует, что тот, или иной переход в то, или иное квантовое состояние - произошел , или может произойти , и вычисляет по определенным правилам
вероятности этих переходов. Но никому, в здравом уме, не придет в голову пытаться выписать "оператор эволюции квантового скачка" (или "оператор эволюции проективного измерения"). Между тем, сделать именно это - предлагает автор задачи, pvp, выписывая свой "оператор эволюции"

в качестве решения этой задачи с, по сути, тем же "квантовым скачком" гамильтониана системы!
-Пытаться проделать такое, это все равно, что пытаться точно сказать в каком именно квантовом состоянии данная квантовая система находится "в процессе" своего квантового скачка (или в процессе проективного измерения над ней.) В то же время, выдавать за "точный оператор эволюции системы" простую "сшивку" операторов квантовой эволюции системы "до" и "после" ее квантового скачка, по меньшей мере, просто безграмотно, поскольку абсолютно неизвестно (и принципиально не может быть известно!) как именно менялось со временем состояние квантовой системы "на протяжении" скачка ее гамильтониана, а значит, тот самый, наиболее определяющий отрезок эволюции квантовой системы, который, собственно говоря, и привел, в действительности, эту систему, от состояния с гамильтонианом

, к состоянию с гамильтонианом

- и который нам принципиально не известен - этот отрезок при такой "сшивке" - попросту "руками выбрасывается" из временной эволюции данной квантовой системы, так как будто его и не было! -Как можно делать "точным начальным условием" для эволюции системы "после" скачка - ее квантовое состояние непосредственно "перед" этим скачком? - А куда делась все то, что происходило с квантовой системой
между этими двумя моментами времени? - Как же может такое быть, что все эти, абсолютно недетерминированные изменения квантового состояния системы, которые, собственно, и изменили ее настолько за этот ничтожный промежуток времени, что она перестала описываться гамильтонианом

и стала описываться гамильтонианом

- как может быть, что все эти кардинальные изменения, будучи, по сути, частью эволюции системы, "не оставили никакого следа" в ее "истинном" операторе эволюции, задающим правильные начальные условия для эволюции системы после скачка гамильтониана? - Очевидно, что "точный оператор квантовой эволюции системы со скачком гамильтониана" - это просто некий нелепый оксюморон! Поэтому

- в принципе, не может быть точным решением поставленной задачи.
(Несколько слов по поводу предельного случая "ультра-больших" скачков гамильтониана системы, напр. при резком и сильном увеличении "управляющего" внешнего поля (как напр. в случае спиновых систем во внешнем магнитном поле). С самого начала, в этом случае интуитивно ясно, что слишком большой скачок гамильтониана - будет соответствовать просто очень большой порции энергии, мгновенно закачиваемой в систему. Но в результате, все что произойдет это то, что данная система просто перестанет быть "квантовой", став "классической", так что в этом случае все квантовомеханические способы ее теоретического описания уже могут быть заменены значительно более простой классической физикой (как например, во всех случаях "жесткой" ориентации спинов в направлении магнитного поля в сильных магнитных полях).
На более строгом теоретическом уровне, можно показать, например, используя идеологию фейнмановских интегралов по траекториям, что, поскольку вклад в действие системы от такого гигантского "скачка" ее гамильтониана - будет огромен по сравнению с

, а действие - это просто фаза пропагатора системы (т.е. ее оператора эволюции) "вдоль конкретной траектории" в пространстве-времени, соответствующей этому значению действия, то любые изменения фаз пропагаторов (т.е. их "вариации"), связанные с любыми "отклонениями" от единственной оптимальной , т.е. "классической" траектории системы - также будут гигантскими, т.е. такие отклонения поведения системы от "классики" будут связаны с сильными осцилляциями квантовых амплитуд соответствующих вероятностей, и, соответственно , такие "отклонения" будут сильно подавлены. В результате, система начнет "вести себя" , в целом, как "классическая" (т.е. полностью детерминированно), но, возможно, с какими-то небольшими квантовыми "поправками", связанными с остающимися малыми отклонениями от ее классического поведения - т.е. с малыми квантовыми флуктуациями.
Примером всего этого может служить , скажем, цепочка взаимодействущих спинов в сильном магнитном поле: В целом при низких температурах, это "существенно квантовая" система с сильным взаимодействием. Однако, если мы начнем увеличивать внешнее постоянное магнитное поле в ней (аналог нашего "скачка"), то, при достаточно большой величине изменения этого внешнего поля - конечный результат для системы будет одним и тем же при любом режиме включения этого постоянного поля - все спины просто будут "заморожены" строго в направлении магнитного поля: так, как будто бы, мы имеем дело не с квантовым объектом - спином, а с его классическим аналогом - макроскопическим магнитным моментом.
-Однако, очевидно, что рассмотрение такого режима "ультра-сильных" скачков гамильтониана в данном случае лишено смысла, т.к. в этом случае изучаемая квантовая система , по сути, разрушается, так что квантовомеханический язык ее описания просто теряет смысл по сравнению с языком "классики". Поэтому мы не будем рассматривать этот случай. А поскольку "промежуточный" случай возмущений достаточно сильных, но при этом не сильно разрушающих квантовую когеренцию в системе, не поддается теоретическому анализу, ниже мы рассмотрим единственный решаемый и наиболее важный в приложениях случай резких скачков гамильтониана системы с достаточно малой амплитудой. О конкретных критериях этой малости см.ниже.)
Легко видеть, что даже в рамках теории возмущений, т.е. при выполнении условий (1,2) общее (теперь уже приближенное) решение поставленной задачи некорректно записывать в виде, предложенном pvp, т.е. в виде

. Причина этого в следующем важном свойстве:
- По условию поставленной задачи, при

гамильтониан системы по-прежнему постоянен (после скачка) и равен:

, где "возмущение"

- есть просто "высота" скачка гамильтониана в момент

. Но тогда, при

временное уравнение Шредингера:

- а, значит, и любое его точное решение в этот момент времени -должно обладать инвариантностью по отношению к обращению времени (с одновременным комплексным сопряжением) (это - фундаментальная симметрия для динамики любых квантовых систем с постоянным гамильтонианом и поэтому она должна выполняться и в этой задаче в пределе

), т.е.

. Отсюда следует, что точный (или правильно приближенный, по теории возмущений ) оператор эволюции данной квантовой системы при

должен удовлетворять условию:

(3)
- выполнение этого условия будет критерием того, что найденный каким-то образом (точно или приближенно) оператор

-правильно описывает квантовую динамику данной квантовой системы.
- Очевидно, что выражение

, предложенное автором задачи, pvp в качестве "точного" решения этой задачи, не удовлетворяет условию (3), т.е.

, (4)
-просто в силу того , что, входящая в фазу

, подынтегральная кусочно-постоянная функция

- определена таким образом на всей оси

, что явно нарушает инвариантность относительно обращения времени (или, что то же самое , трансляционную инвариантность по времени), т.к.

. (5)
Однако, рассматривая, как малое возмущение (в силу выполнения условий (1,2)) оператор

в правой части бесконечного разложения Дайсона для точного оператора эволюции системы

в представлении взаимодействия по

(и, приравнивая для простоты:
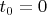
) и ограничиваясь в этом разложении членами до 2-го порядка включительно, после интегрирования по времени, будем иметь приближенно (в силу выполнения условий(1,2))

(6)
где:

Очевидно, найденный нами по теории возмущений приближенный оператор эволюции

из выражения (6) - удовлетворяет условию (3), т.е. найденное нами таким образом решение задачи обладает требуемой симметрией относительно обращения времени и, следовательно, правильно описывает эволюцию квантовой системы под действием малого скачкообразного изменения ее гамильтониана