Об ещё одной конструкции структурного пучка аффинной схемы

[kp9r4d]

У меня вопрос по следующему ответу на МО:

Цитата:

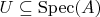
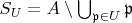
For any open subset $U\subseteq\mathrm{Spec}(A)$ let $S_U=A\setminus\bigcup_{\mathfrak p\in U}\mathfrak p$ and $\mathscr O'(U)=A[S_U^{-1}]$. It is obviously a presheaf.

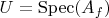
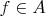
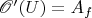
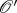
Claim: For open subsets of the form $U=\mathrm{Spec}(A_f)$ with $f\in A$ we have $\mathscr O'(U)=A_f$. (This shows that the associated sheaf of $\mathscr O'$ is indeed $\mathscr O_{\mathrm{Spec}(A)}$.)

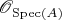
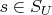
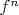
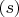
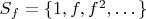
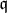
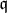
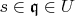
Proof: Assume there is an $s\in S_U$ which does not divide $f^n$ for any $n$. The ideal $(s)$ does not meet the multiplicative set $S_f=\{1,f,f^2,\dots\}$, so it is contained in an ideal $\mathfrak q$ which is maximal with respect to this property, but it is well-known that such an ideal $\mathfrak q$ is prime. By construction, $s\in\mathfrak q\in U$, contradicting $s\in S_U$.

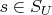
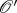
Applying the usual associated sheaf construction to $\mathscr O'$ seems to be what Hartshorne does when he defines $\mathscr O_{\mathrm{Spec}(A)}$.

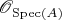
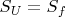
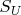
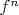
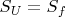
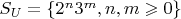
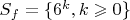
Я как понял, основная идея, это показать, что $S_U = S_f$. Но разве из того, что в $S_U$ нету ни одного элемента $s$ такого, что $s$ не делит $f^n$ для любого $n$, следует, что $S_U = S_f$? Грубого говоря, если взять $S_U = \{2^n 3^m, n,m \geqslant 0\}$, а $S_f = \{6^k, k \geqslant 0\}$, разве не будет это контрпримером?

[Xaositect]

Да, это работает только для неприводимого $f$.
Но, насколько я понимаю, там именно это и нужно. Для главных (principal) открытых множеств все хорошо, а для неглавных нам нужна как раз именно эта локализация по большому мультипликативному множеству всех не обращающихся в 0 функций.

[kp9r4d]

Xaositect в сообщении #1175652 писал(а):

Для главных (principal) открытых множеств все хорошо,

Мне, грубо, и непонятно, почему для главных всё хорошо. Там разве и не доказывается, то, что $S_{D(f)} = S_f$?

[Xaositect]

Ой, я перепутал. Имел в виду главные открытые множества с неприводимым $f$ или степенью неприводимого.

[kp9r4d]

Так а для колец, которые не integral domain неприводимость имеет смысл разве?

[Xaositect]

Да, Вы правы, как-то слишком много предположений получается.

Не достаточно ли того, что доказано ($S_U = S_{D(f)}$) для того, что требуется? У нас же над главным открытых множеством нужно как раз кольцо $A_{D(f)}$, локализация по тем элементам, которые на нем в 0 не обращаются.

[kp9r4d]

Xaositect в сообщении #1175686 писал(а):

Не достаточно ли того, что доказано ($S_U = S_{D(f)}$) для того, что требуется?

Да достаточно, конечно, ведь $D(f)$ образуют базу у $\operatorname{Spec} A$, мне непонятно, почему это доказано. Точнее непонятно, почему $S_{D(f)}=S_f$, ($S_U = S_{D(f)}$ - это определение $U$ вроде)

[Xaositect]

А они не равны, Вы же привели пример в первом сообщении. Но может быть нам на самом деле нужны $S_{D(f)}$, а не $S_f$?

[kp9r4d]

Но мой пример не подходит, $\{2^n 3^m, n,m \geqslant 0\}$ не является множеством типа $S_{D(f)}$ ни для какого $f$.

-- 10.12.2016, 15:29 --

Я разобрался если мультипликативные множества $A,B \subset R$ такие, что для любого $a \in A$ существует $b \in B$ такой, что $a$ делит $b$, то $A$ и $B$ хоть могут быть и не равны, но локализации по ним всегда равны $R[A^{-1}]=R[B^{-1}]$, а ровно это и нужно. Спасибо в любом случае ^^