В Теореме Гаусса используется понятие телесного угла. Телесный угол вырезает некоторую площадь, под которой виден некоторый элемент поверхности. ...
Обратите внимание на теорему, в ней говорится про некий поток. Вот и пользуйтесь гидродинамической аналогией. Т.е. не старайтесь увидеть площадь в телесном угле, а представьте, что через эту площадь течет поток "жидкости". Теперь необходимо вспомнить, что поток через площадь равен произведению нормальной составляющей потока на площадь.
Например так:
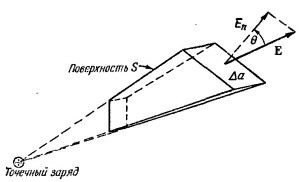
т.е. площадь, из которой выходит поток, за счет большего наклона больше, но в то же самое время и нормальная составляющая потока меньше. Из таких маленьких площадок можете составить поверхность произвольной формы.
Если телесным углом вырезать кусок поверхности сферы, то эл. поле будет во всех точках перпендикулярно такой поверхности, и поток находим как произведение сферической площади на значение эл. поля на этой поверхности (естественно во всех точках такой сферической поверхности значение поля будет одинаковым).
Но если телесным углом вырезать кусок поверхности куба с тем же радиусом, как и для сферической поверхности, то уже значение нормальной составляющей поля на такой плоской поверхности в разных точках будет разным, в среднем значение поля будет больше, т.к. такая поверхность находится ближе к точечному заряду, но и сама площадь будет меньше (это "тень" от предыдущей сферической поверхности, и потоки через эти поверхности будут равны). Поэтому аналогия с тенью есть, но надо учитывать "что на что умножать".



