А перерисуйте-ка в осях

? Интересно, как выглядеть будет.
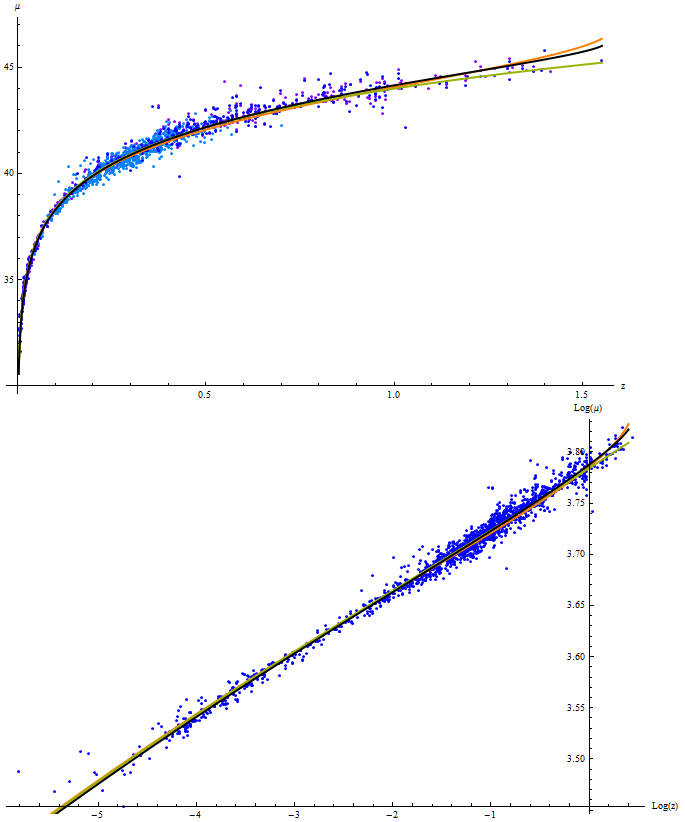 Зелёная
Зелёная - это де Ситтер



световых лет. Среднеквадратичное отклонение графика

от точек получилось

. Момент времени

ничем не выделен. Есть сингулярность при

.
Рыжая - это мало кому известная открытая модель Фридмана с "отрицательной энергией". Интересна тем, что расширяется ускоренно и не имеет сингулярности.



световых лет. После момента максимального сжатия (несингулярного!!!) прошло

лет. Среднеквадратичное отклонение графика

от точек получилось

.
Чёрная - это простейшая модификация де Ситтера с выделенным моментом времени

. Как и рыжая тоже с "отрицательной энергией" и тоже не имеет сингулярности. При

стремится к модели де Ситтера.



световых лет. После момента максимального сжатия (несингулярного!!!) прошло

лет. Среднеквадратичное отклонение графика

от точек получилось

(лучший результат).
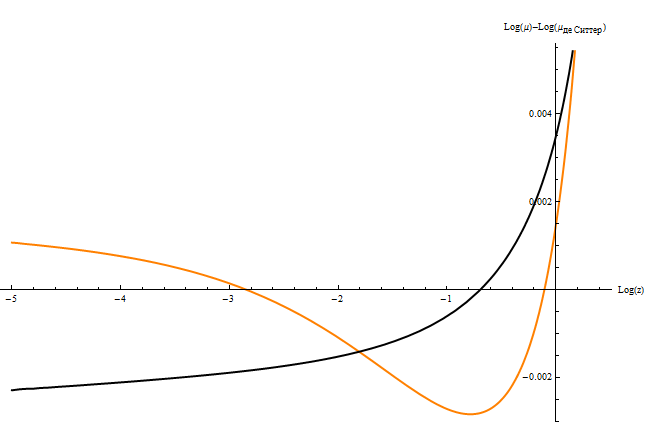
У обеих рассмотренных несингулярных моделей расширяющихся с ускорением хвост графика

торчит вверх при больших

. Отклонение рыжей и чёрной кривых от зелёной кривой де Ситтера: