А простые числа Вы берете в первой степени или произвольной?
Если только в первой степени, то уже числа, делящиеся на степень простого, выпадают из Вашего 'все'.
Для них, получается, нужно отдельное 'доказательство.'
Eller hur? (или как еще? (шв.))
Скоро я буду говорить на Шведском. Det är endast första nödvändigt till minskning (шв., только сначала необходимо уменьшить )количество ляпсусов на русском. Однажды автомат перевел мне фразу «Дорогу осилит идущий» на английский как “Всегда найдется выход из тупика тупикового".
Уважаемая Shwedka!
Случай, когда

, не нарушает общности утверждения, что после произвольного деления образуются все составные кубы с общим делителем, кроме куба являющегося произведением всех кубов для полуинтервала простых чисел
![$(1,P_i]$ $(1,P_i]$](https://dxdy-04.korotkov.co.uk/f/7/c/4/7c48ecd0fc19203b1ac745c48c5fb5c782.png)
. Увеличивается число исходов до произвольного деления. Точно также увеличивается число исходов после деления.
Благодаря такому определению, можно сократить текст и перейти сразу же к произвольному

-шагу бесконечного спуска.
Имеем множество всех простых чисел в полуинтервале
![$(1, P_i]$ $(1, P_i]$](https://dxdy-01.korotkov.co.uk/f/c/7/0/c70c5b8b287b5210d706f7c519d07f2882.png)
.
Произвольным сочетанием простых чисел из
![$(1, P_i]$ $(1, P_i]$](https://dxdy-01.korotkov.co.uk/f/c/7/0/c70c5b8b287b5210d706f7c519d07f2882.png)
образуем их произведение - число

и взаимно простое с ним число

.
В случае если не существует решений для УФ3, имеем составной куб

с общим делителем

, для других кубов УФ3,
В результате такого произвольного деления образуются все составные кубы, получаемые сочетанием кубов по
![$(1,P_i] $ $(1,P_i] $](https://dxdy-01.korotkov.co.uk/f/0/3/9/039833c92b460037046794ad193106eb82.png)
, кроме куба - произведения всех простых чисел
![$(1,P_i]$ $(1,P_i]$](https://dxdy-04.korotkov.co.uk/f/7/c/4/7c48ecd0fc19203b1ac745c48c5fb5c782.png)
Составим тождество]

Правая часть (1) не может быть суммой двух кубов, так как в этом случае выражение в скобках

должно быть кубом. То есть

Обратим внимание на то, что (2) охватывает все составные кубы с общим делителем, созданные произвольными произведениями простых чисел из
![$(1, P_i]$ $(1, P_i]$](https://dxdy-01.korotkov.co.uk/f/c/7/0/c70c5b8b287b5210d706f7c519d07f2882.png)
, кроме одного куба - произведения всех кубов простых чисел
![$(1, P_i]$ $(1, P_i]$](https://dxdy-01.korotkov.co.uk/f/c/7/0/c70c5b8b287b5210d706f7c519d07f2882.png)
. Поэтому (2) имеет все свойства (1). Так как для куба - произведения всех кубов
![$(1,P_i]$ $(1,P_i]$](https://dxdy-04.korotkov.co.uk/f/7/c/4/7c48ecd0fc19203b1ac745c48c5fb5c782.png)
уже имеется утверждение, что согласно (1), этот куб не может быть суммой двух других кубов.
Поэтому справедливо утверждение, что выражение в скобках в (2)

не может быть кубом, так как в противном случае, аналогично выводам в (2), существовало бы следующее решение УФ3 с общим делителем и так до бесконечности. Но не существует бесконечности кубов натуральных чисел, меньших заданного куба натурального числа.
Таким образом, ни какой куб с общим делителем для других кубов УФ3 не существует. Следовательно, не существует и взаимно простых решений для УФ3, а также для всех других степеней с простым показателем
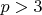
Для этого в тексте необходимо заменить всего один символ 3 на

, а слово куб - на слово степень.