
Если Вы имеете в виду кубическую кривую, то Ваш график не бывает.
Дело не только в многозначности к.Б. Рассмотрите кривую с опорными точками

,

,
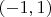
,

(с петлёй). Если мы возьмём точку на петле, и начнём двигаться вправо, то

будет меняться непрерывно как функция

. До

. В этот момент станет меняться некуда, и произойдёт перескок на нижнюю ветку.
artful7 писал(а):
Поскольку значение параметра t лежит в интервале [0, 1], то следовательно, значение t - непрерывная величина и (теоретически) можно задать любое ее значение.
Что-то очень непонятное. К.Б. — множество точек

для
всех ![$t \in [0,1]$ $t \in [0,1]$](https://dxdy-01.korotkov.co.uk/f/0/1/d/01df98f22b2b1c9a0c617975dfbe543c82.png)
. Без всяких
теоретически.



