Спасибо за помощь, извиняюсь за задержку. Разобрался с этим, выкладываю всё доказательство подробно. Ещё нужно было доказать, что башня после уплотнения остаётся абелевой. Надеюсь, всё правильно.
Пусть есть абелева башня

.
1) Рассмотрим факторгруппу

. Так как она абелева, то для неё можно построить башню с циклическими факторами, где наименьшая подгруппа тривиальная. Так как если

,

- факторгруппа и

- подгруппа

, то

, где

- какая-то подгруппа


, эту башню можно записать следующим образом:

, где

- подгруппы
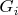
. Группы
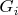
и

связаны каноническим гомоморфизмом

, поэтому прообраз циклической башни в

образует циклическую башню в
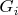
:

. Таким образом уплотняется вся башня.
2) Докажем ещё, что после нашего циклического уплотнения башня остаётся абелевой.

,

- абелева факторгруппа, поскольку является подгруппой

. Далее, для гомоморфизма


,

ядром будет

, (Ленг. Нормальные подгруппы, стр. 30, пункт (iii)) поэтому

.
Факторгруппа

изоморфна

, (про этот изоморфизм в том же пункте у Ленга) откуда следует, что

- абелева факторгруппа для

.

- абелева, т.к. она есть подгруппа

.
(Оффтоп)
Что-то такое чувство, что у меня в конспекте учебник, а у Ленга - набросок этого учебника: по ощущениям чуть ли не 90% утверждений нужно доказывать самостоятельно.



