Всем привет! У меня есть некотрых вопрос по такой, пожалуй, классическое задачи:
Цитата:
Один конец тонкой гибкой верёвки с линейной плотностью

тянут с постоянной горизонтальной скоростью на высоте

над шероховатой поверхностью. Второй конец верёвки свободен и лежит на поверхности. Длина части верёвки, соприкасающейся с поверхностью, равна

. Найдите длину верёвки

, не касающейся поверхности. Коэффициент трения скольжения верёвки по поверхности равен

. (см. рис. слева)
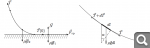
Рассмотрим маленький кусочек верёвки, находящейся в воздухе. (рис. справа) Тогда по II з-ну Ньютона в проекции на тангенциальное направление выполняется:

. (1). Проинтегрируем обе части равенства от нуля до

по

. Тогда получится, что разность силы натяжения в самой высокой и самой низкой части висящего куска веревки отличаются на величину

.
В авторском решении задачи из (1) следует буквально, что та самая разность силы натяжения в самой высоко и самой низкой части висящего куска веревки отличаются на величину

, то есть зависит от синуса угла. Выходит, проинтегрировала неправильно? Почему? Да и разве можно утверждать, что

, ведь верёвка именно
провисает, а значит угол между касательной и висящей частью веревки будет меньше

.
|
i |
Pphantom: |
| Поправил опечатку в заголовке темы. |



