Обозначим нашу форму

.
Насколько я понимаю, чтобы проверить инвариантность, нужно проверить что производная Ли от формы

вдоль векторного поля отображения Пуанкаре равна нулю.
Совершенно верно. В частности, это гарантирует, что если какая-то интегральная кривая поля

, выйдя из точки

, вернётся через один или несколько оборотов в ту же точку

, то форма

, полученная из

в той же точке с помощью переноса потоком, совпадёт с

.
Воспользуемся дважды тождеством Картана (оно же формула гомотопии). Сначала применим его к форме

:

Слева нуль в силу инвариантности

. Справа первое слагаемое равно нулю, так как

— ненулевая форма максимально возможной степени, и
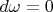
. Следовательно, и

.
Теперь применим тождество Картана к

:

В правой части первое слагаемое нулевое, т.к.

, а второе равно нулю в силу кососимметричности форм (два совпадающих векторных аргумента). Следовательно,




