Неоднородное уравнение теплопроводности

[Borisko]

Здравствуйте.
Имеется задача:
${u}_{t}=a{u}_{yy}+A(y,t)+c(t)\\u(y,0)=0\\u(0,t)=u(l,t)=0\\\int_{0}^{l}u(y,t)dy=q(t)\\$

Подскажите смогу я решить ее методом Фурье? Функция A(y,t) найдена (также методом разделения переменных), а функция c(t) определяется из дополнительного интегрального условия; q(t) известна.

[Red_Herring]

Разложите и $u(y,t)$ и $A(y,t)$ и даже $c(t)$ по соотвествующим собственным функциям (каким?) и найдите коэффициенты.

[Borisko]

Конечно я могу разложить все функцию (по синусам)... Вопрос не помешает ли мне интегральное условие? То есть могу ли я найти решение для u а потом поставить решении в интегральное условие и выразить c(t) через q(t)?

[Red_Herring]

Пусть $u_1(x,t)$ решение стандартной задачи с $c(t)=0$ и без последнего условия. Тогда Вы легко можете найти $q_1(t)=\int_0^l u_1(x,t)\,dx$. Тогда $u=u_1+v$, где $v $ решение Вашей задачи с $A=0$ и $q$ заменено на $q-q_1$.

Поробуйте решить эту упрощенную задачу

[ewert]

Borisko в сообщении #1131684 писал(а):

Имеется задача:
${u}_{t}=a{u}_{yy}+A(y,t)+c(t)\\u(y,0)=0\\u(0,t)=u(l,t)=0\\\int_{0}^{l}u(y,t)dy=q(t)\\$

Смогли бы, если бы задача не была переопределена: первые три строчки задают решение уже однозначно.

[Borisko]

ewert в сообщении #1131803 писал(а):

Borisko в сообщении #1131684 писал(а):

Имеется задача:
${u}_{t}=a{u}_{yy}+A(y,t)+c(t)\\u(y,0)=0\\u(0,t)=u(l,t)=0\\\int_{0}^{l}u(y,t)dy=q(t)\\$

Смогли бы, если бы задача не была переопределена: первые три строчки задают решение уже однозначно.

Так c(t) неизвестная функция. И определимся вместе решением.

-- 15.06.2016, 19:48 --

Red_Herring в сообщении #1131755 писал(а):

Пусть $u_1(x,t)$ решение стандартной задачи с $c(t)=0$ и без последнего условия. Тогда Вы легко можете найти $q_1(t)=\int_0^l u_1(x,t)\,dx$. Тогда $u=u_1+v$, где $v $ решение Вашей задачи с $A=0$ и $q$ заменено на $q-q_1$.

Поробуйте решить эту упрощенную задачу

Так получается в задаче для v последнее условие останется? И будет тоже самое, что и для u. Только A=0 и все?

[Red_Herring]

В задаче для $v$ последнее условие и $c(t)$ остаются, но $A=0$ и $q$ изменяется (из него вычитается то, что получилось для $A$). Будем рассматривать Вашу задачу с $A=0$. И пусть для простоты $\alpha=1$ и $l=\pi$. Тогда будет $u(x,t)=\sum U_n(t) \sin (nx)$, $c(t)= \sum c(t) k_n \sin(nx)$ и $q(t)= \sum q(t) k_n \sin(nx)$, где $k_n$ коэффициенты разложения $1$, т.е. $k_n=4/\pi n$ для нечетных $n$ и 0 для четных, т.е. везде $n$ нечетное.

Выразите $U_n(t$) через $c(t)$ и подставьте в $q(t)$; получите интегральное уравнение для $c(t)$. Можно (и наверно лучше) сделать преобразование Лапласа по $t$ для решения ОДУ для $U_n(t)$ и подстановки в п.Л. для $q(t)$

[Borisko]

Red_Herring в сообщении #1131831 писал(а):

В задаче для $v$ последнее условие и $c(t)$ остаются, но $A=0$ и $q$ изменяется (из него вычитается то, что получилось для $A$). Будем рассматривать Вашу задачу с $A=0$. И пусть для простоты $\alpha=1$ и $l=\pi$. Тогда будет $u(x,t)=\sum U_n(t) \sin (nx)$, $c(t)= \sum c(t) k_n \sin(nx)$ и $q(t)= \sum q(t) k_n \sin(nx)$, где $k_n$ коэффициенты разложения $1$, т.е. $k_n=4/\pi n$ для нечетных $n$ и 0 для четных, т.е. везде $n$ нечетное.

Выразите $U_n(t$) через $c(t)$ и подставьте в $q(t)$; получите интегральное уравнение для $c(t)$. Можно (и наверно лучше) сделать преобразование Лапласа по $t$ для решения ОДУ для $U_n(t)$ и подстановки в п.Л. для $q(t)$

Получается на $c(t)$ как ни решай будет получаться интегральное уравнение? то есть явно записать не получиться.

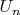
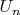
и как $U_n$ выразить через $c(t)$ если в $U_n$ содержится интеграл от $c(t)$... или я чего то не понимаю...

-- 22.06.2016, 11:34 --

Я решала методом преобразования Лапласа. Можно было сразу найти решение для $u$ (но численно), а мне нужно выписать решение для $u$ в явном виде (в виде рядов), чтобы решить следующую задачу. Так как в следующей задаче в уравнении параболического типа правая часть есть произведение $A(y,t)u(y,t)$. А найти изображение от произведения нельзя..

[Red_Herring]

УЧП решаются в явном виде при исключительном везении. А просто ри большом везении они сводятся к уравнениям меньшей размерности и у Вас именно последний случай.

Итак: $u_t =u_{xx} +c(t), \qquad, u(0,t)=u(\pi,t)=0,\qquad u(x,0)= g(x)$ и $\int_0^\pi u(x,t)\,dx =q(t)$.
Даны: $g(x)$ и $q(t)$, найти $u(x,t)$ и $c(t)$.

Поскольку $1=\sum_{n} \frac{4}{\pi n} \sin{n x}$ с суммированием везде по нечетным $n$ то с четными $n$ все стандартно, и будем считать, что $g(x)=\sum_n g_n\sin(nx)$ тоже с нечетными $n$ .

Будем искать $u(x,t)=\sum_n u_n(t) \sin (nx)$ и что мы имеем: $u_n' +n^2 u_n = \frac{4}{\pi n} c(t), \qquad u_n(0)=g_n$, и $\sum_n \frac{2}{n} u_n(t) = q(t)$.

После преобразования Лапласа имеем
$(\tau +n^2)U_n(\tau)= \frac{4}{\pi n} C(\tau) + g_n$ и тогда
$U_n(\tau)= \frac{4}{\pi n (\tau +n^2)} C(\tau) + \frac{1}{(\tau +n^2)} g_n$ и подставляя в
$\sum_n \frac{4}{\pi n} U_n = Q(\tau)$ получим
$\sum_n \frac{8}{\pi n^2 (\tau +n^2)} C(\tau) + \frac{2}{n(\tau +n^2)} g_n = Q(\tau)$.

Отсюда находим

$$C(\tau)= \frac{ -\sum_n \frac{2}{n(\tau +n^2)} g_n + Q(\tau)}{\sum_n \frac{8}{\pi n^2 (\tau +n^2)} } $$

и т.д. Это наиболее явный ответ.

[Borisko]

Red_Herring в сообщении #1133329 писал(а):

$U_n(\tau)= \frac{4}{\pi n (\tau +n^2)} C(\tau) + \frac{1}{(\tau +n^2)} g_n$ и подставляя в
$\sum_n \frac{4}{\pi n} U_n = Q(\tau)$ получим
$\sum_n \frac{8}{\pi n^2 (\tau +n^2)} C(\tau) + \frac{2}{n(\tau +n^2)} g_n = Q(\tau)$.

Отсюда находим

$$C(\tau)= \frac{ -\sum_n \frac{2}{n(\tau +n^2)} g_n + Q(\tau)}{\sum_n \frac{8}{\pi n^2 (\tau +n^2)} } $$

и т.д. Это наиболее явный ответ.

А получится взять обратное преобразования Лапласа и найти оригинал? (начальные данные нулевые)

-- 23.06.2016, 04:18 --

Например использовать теорему умножения. Если g(x)=0 и произведение изоброжений равно свертки оригиналов. А оригинал для Q(tau) есть q(t)

[Red_Herring]

Borisko в сообщении #1133458 писал(а):

А получится взять обратное преобразования Лапласа и найти оригинал? (начальные данные нулевые)

Например использовать теорему умножения. Если g(x)=0 и произведение изоброжений равно свертки оригиналов.

Ну а каков оригинал $\Bigl( \sum_n \frac{8}{\pi n^2 (\tau+n^2)}\Bigr)^{-1} $? Я не знаю и сомневаюсь, что кто-нибудь в нашей Галактике знает. Дело тут отнюдь не в начальных данных.

Напоминаю: суммирование по нечётным $n$

[Borisko]

Red_Herring в сообщении #1133459 писал(а):

Borisko в сообщении #1133458 писал(а):

А получится взять обратное преобразования Лапласа и найти оригинал? (начальные данные нулевые)

Например использовать теорему умножения. Если g(x)=0 и произведение изоброжений равно свертки оригиналов.

Ну а каков оригинал $\Bigl( \sum_n \frac{8}{\pi n^2 (\tau+n^2)}\Bigr)^{-1} $? Я не знаю и сомневаюсь, что кто-нибудь в нашей Галактике знает. Дело тут отнюдь не в начальных данных.

Напоминаю: суммирование по нечётным $n$

Значит опять тупик и без преобразования Лапласа никуда? Не может же быть часть решения в изображениях а часть в оригиналах..

[sup]

А что, решение нужно обязательно в явном (формульном) виде? Или же нужен просто некий вид, удобный для дальнейшего анализа?
Вообще говоря, задачи такого рода сводятся и эквивалентны интегральным уравнениям Вольтерра первого рода. В Вашем случае получается уравнение сверточного вида, а значит хотя бы решается с помощью преобразования Лапласа. Если бы в правой части стояло слагаемое $c(t)F(y,t)$, то шансы на хоть какое-то явное решение были бы равны 0.

[Red_Herring]

Если бы $1$ была собственной функцией (что будет при Неймановских граничных условиях), то всё было бы легко. А так у Вас все коэффициенты при собственных функциях запутаны и мы имеем просто "большое везение", а не "исключительное везение".

Borisko в сообщении #1133460 писал(а):

Не может же быть часть решения в изображениях а часть в оригиналах..

Нет, решение выглядит так : $ u=\sum u_n(t) \sin (nx)$ где $u_n(t)$ оригиналы $U_n(\tau)$ определенных выше.

[Borisko]

Вроде поняла как решать. Нашла то, что мне надо в одной статье... только не могу разобраться в одном месте... помогите пожалуйста. Там написано: $\lambda_k$ это к-ый положительный корень уравнения $\tg\lambda_k=\lambda_k$, $\lambda_k\to (2k+1)\pi/2, k\to \infty$. И написано, что $\sin\lambda_k=\frac{\lambda_k}{\sqrt{1+\lambda_k^2}}$. Как это получилось? тогда получается, что $\cos\lambda_k=\frac{1}{\sqrt{1+\lambda_k^2}}$?