Почему как только мы прицепляем к каждой вероятности фазу мы получаем исчерпывающее описание состояния системы? Почему именно фазу и почему фазы достаточно? За этим должно стоять что-то очень простое и фундаментальное.
За этим стоит теория групп, а конкретнее - понятие об унитарных неприводимых представлениях (НП) однопараметрических групп преобразований...
Вспомните, как ребёнок познаёт мир? Он пробует разобрать каждую игрушку на части: посмотреть, из чего она состоит. А как Вы узнаёте, что окружающий мир состоит из частей? Так же: подвергаете наблюдаемую картину преобразованиям - вертите перед глазами всё на разные углы

, двигаете ближе-дальше на разные расcстояния

, повторяете опыты через разные промежутки времени

И замечаете тем самым, что мир состоит из частей: составная часть это то, что преобразуется неприводимо (т.е. независимо от других частей) по отношению к заданному виду преобразований.
Та же идея на языке математики: мы предполагаем, что "элементарные части мира" в теории следует описывать функциями (векторами состояний, амплитудами вероятности), реализующими НП групп преобразований.
1) Для примера рассмотрите группу операторов сдвига

какого-либо квантового объекта вдоль декартовой оси

на расстояние

Ясно, что "облако амплитуды вероятности"

при таком сдвиге превращается в

Теория групп учит: НП в данном случае должны быть одномерными. Т.е. самые элементарные (по отношению к сдвигам) функции

это те,
которые при сдвиге просто-напросто умножаются на числа. Поскольку

имеет смысл плотности вероятности, то она не должна при сдвиге облака вероятности "к краю вселенной" неограниченно расти, и поэтому нам не подходят функции типа

или

с вещественным параметром

в показателе. Подходят только функции с мнимым показателем, т.е. имеющие вид (с точностью до произвольного нормировочного множителя):

Такими функциями реализуются унитарные НП группы операторов

Попросту говоря, такие функции ограничены и при сдвиге лишь умножаются на число, без изменения функциональной зависимости от координаты:

переходит в

Важный экспериментальный факт о нашем мире: сдвиги вдоль разных направлений коммутативны. Следствие этой коммутативности: унитарные НП группы трёхмерных сдвигов

одномерны и реализуются экспоненциальными функциями с мнимым показателем:

Действительно, при сдвиге каждая такая функция с любым векторм

просто умножается на число


В квантовой теории такие функции

называются плоскими волнами и применяются для описания "состояний квантовой частицы с определённым импульсом"; векторный параметр

по определению называется "импульсом" в единицах обратной длины. В качестве дополнительного упражнения Вы можете убедиться, что оператор сдвига допускает запись в виде

где оператор

называется "оператором импульса" (в единицах обратной длины), причём функции

удовлетворяют уравнению:

2) Аналогично рассмотрите в группе трёхмерных вращений подгруппу операторов поворота

какого-либо квантового объекта на всевозможные углы

вокруг декартовой оси

Унитарные НП этой подгруппы одномерны и реализуются функциями, зависящими от азимутального угла

сферической системы координат

тоже по закону экспоненты с мнимым показателем:

ибо тем самым при повороте вокруг оси

обеспечивается просто-напросто умножение такой функции на число:

Присутствующий здесь параметр

в КМ по определению называется проекцией

орбитального момента импульса

на ось

в безразмерных единицах.
Важный экспериментальный факт о нашем мире: повороты вокруг различных направлений в общем случае некоммутативны. Как следствие, НП для группы трёхмерных вращений устроены сложнее, чем для группы сдвигов. Базисные функции НП группы вращений нумеруются не вектором

, а парой чисел

где число

в КМ называется "величиной орбитального момента" в безразмерных единицах. При заданном

базисные функции НП составляют

-мерный мультиплет с

Функции в каждом мультиплете при поворотах линейно преобразуются друг через друга, не смешиваясь с функциями из других мультиплетов. Детальный анализ показывает, что зависимость от угла

у функций в мультиплете даётся известными в математике присоединёнными функциями Лежандра

так что с точностью до нормировочного множителя базисные функции НП группы вращений имеют вид:

где радиальная часть

не определяется группой вращений; индекс
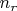
здесь служит для нумерации линейно независимых радиальных функций в мультиплете с заданным

. Угловую часть с надлежащими нормировочными множителями принято обозначать как


В КМ фундаментальную роль играют ещё и "двузначные НП" (спинорные представления) группы трёхмерных поворотов - это основа квантового понятия о
спиновом моменте импульса электронов и атомных ядер, и о
принципе запрета Паули; не стану комкать этот важный сюжет в "штрих-пунктирное" изложение.
3) Наконец, рассмотрите группу сдвигов вдоль оси времени

. Сдвиг на временной интервал

играет роль оператора эволюции

превращающего

в

Эволюция квантового состояния от

до

т.е. от нулевого момента времени до времени

описывается как результат применения к

оператора эволюции

Очевидно, по аналогии со сдвигами вдоль пространствнной оси, здесь НП даются экспонентами с мнимым показателем:

ибо при сдвиге вдоль оси времени такая функция просто-напросто умножается на число:

В квантовой теории параметр

по определению называется "энергией" в единицах частоты.
При этом опыты обнаруживают
чудо: удаётся из опытов вычислить
универсальную (одинаковую для всех квантовых объектов!) константу

такую, что она превращает квантовые размерности механических величин в классические размерности, установленные задолго до открытия КМ:

- импульс в классических единицах импульса,

- момент импульса в классических единицах момента импульса,

- энергия в классических единицах энергии.
Это важный факт в анализе происхождения законов классической механики. Важный наряду с теоремами Эренфеста (показывающими, как формулы классической механики возникают "в среднем по квантовым состояниям") и важный наряду с интегралом по траекториям Фейнмана (показывающим происхождение принципа наименьшего действия в классической механике). Этот круг идей можно назвать
принципом соответствия классической механики квантовой механике; из него следует гипотеза в КМ, согласно которой "по образу и подобию" классической функции Гамильтона

для конкретной модели можно строить
оператор энергии 
квантового объекта, эволюционирующего в однородном времени

. При этом оператор эволюции есть

Соберём теперь всё вместе, притом не брезгуя данными опытов. Рассмотрим в качестве "элементарных частей" окружающего нас мира известные из опыта атомы, с их электронами и ядрами. Если электрон в атоме находится в стационарном состоянии в сферически симметричных условиях, то разумно думать, что тогда допустимые для него волновые функции (
орбитали) реализуют НП группы трёхмерных поворотов и сдвигов во времени:

Очевидно, параметр

здесь не произволен, а определяется уравнением (с надлежащими граничными условиями):

где, как мы уже знаем,

причём функция

универсальна - она не зависит от формы сферически симметричного потенциала

в гамильтониане

Эта же симметрия гарантирует, что допустимые значения энергии

не зависят от проекции момента импульса

т.е.

Фактически, здесь уравнение Шрёдингера

сводится к обыкновенному дифференциальному уравнению для радиальной части орбитальной волновой функции, и анализ показывает, что:
а) номером
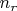
служит число "узлов" радиальной функции:

,
б) в разумных моделях атома оказывается, что с неплохой точностью значения одноэлектронных уровней энергии

сильно зависят только от суммы вида

а не в отдельности от "квантовых чисел"
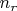
и

Тогда, с учётом количества

допустимых значений

имеем

одноэлектронных орбиталей с почти совпадающими значениями энергии

Поскольку на каждой орбитали

электрон может находиться в любом из
двух состояний, различающихся проекцией спина, а в пренебрежении магнитным полем спин не влияет на энергию электрона, то имеется

одноэлектронных квантовых состояний с близкими значениями одноэлектронной энергии с заданным

Вместе с принципом Паули этот факт в итоге ведёт нас к пониманию происхождения "Периодической системы элементов"- важнейшего эмпирического закона о строении нашего мира в терминах химии!
Мораль: свойства атомов, как составных частей окружающего нас мира, почти полностью определяются их симметрией по отношению к трёхмерным поворотам. Анализ таких, казалось бы, мелких деталей, как электронные "орбитали", оказался важным для понимания свойств мира! Комплексные функции появляются в квантовой теории по простым, но фундаментальным причинам: это проявление групп симметрии в математическом аппарате КМ. При этом КМ вскрывает связь между основными физическими величинами (импульс, момент импульса, энергия) и симметриями пространства (однородность, изотропия) и времени (однородность) более явно, чем классическая механика; а сама классическая механика представляется в некотором смысле "предельным случаем" КМ.
Подобным же образом, т.е. на основе анализа симметрии, строится КМ-теория молекул (см. ЛЛ-3). Овладев этой идеологией и соответствующим математическим инструментарием, Вы поймёте, что отчасти аналогичным образом идеи симметрии способствуют проникновению человеческого разума в тайны строения микромира и на масштабах, много меньших размера атомов!



