Общий перпендикуляр

[gefest_md]

Расходящиеся прямые имеют точно один общий перпендикуляр. Я убеждён, что перпендикуляр существует, но хочется получить подтверждение эксперта, что я правильно понял доказательство. Кажется что прямые двигаются при попытке ткнуть карандашом в прямую $b.$

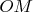
Итак пусть $a$ и $b$ какие-нибудь расходящиеся прямые ($b$ выше $a$). Беру точку $O$ на прямой $b$. Опускаю перпендикуляр $OA$ к прямой $a$. Перпендикуляр $OA$ и прямая $b$ образуют тупой и острый углы (рассматриваю этот случай). Задаю функцию. Для любой точки $M$ прямой $b$, длине $|x|$ отрезка $OM$ ставлю в соответствие длину перпендикуляра $MN$ к прямой $a$. И вот, что я понял.
1. функция непрерывна, монотонна, возрастающая, неограниченна со стороны тупого угла.
2. функция непрерывна и неограниченна со стороны острого угла.
3. минимальное значение функции ($f(x_0)$) есть длина отрезка, совпадающего с общим перпендикуляром.
4. общий перпендикуляр находится со стороны острого угла.
Скажите, пожалуйста, если я всё правильно понял.

[Brukvalub]

Расходящиеся $=$ скрещивающиеся?

[grizzly]

Brukvalub в сообщении #1116479 писал(а):

Расходящиеся $=$ скрещивающиеся?

Нет, там про геометрию Лобачевского (по секрету :)

[gefest_md]

Через точку вне прямой проходят две параллельные прямые (правая и левая) и бесконечно много расходящихся. По-видимому отношение расходимости симметрично, что следует из симметричности отношения параллельности.

[grizzly]

gefest_md в сообщении #1116478 писал(а):

длине $|x|$ отрезка $OM$ ставлю в соответствие длину перпендикуляра $MN$ к прямой $a$

Можете ли Вы чуть формальнее записать Вашу функцию? А то создаётся впечатление, что либо Вы рассматриваете многозначную функцию, либо у Вас на самом деле функция двух аргументов ($|x|$ и "тупость / острота угла").

[gefest_md]

Вся прямая $b$ становится координатной осью с центром $O$. Число $x$ - это координата произвольной точки $M$ на оси. Число $f(x)$ - есть длина перпендикуляра $MN$, опущенного на другую прямую $a$. Функция однозначна, что следует из единственности перпендикуляра $MN$.

-- Пн апр 18, 2016 22:48:08 --

Если угол при точке $O$ прямой, то общий перпендикуляр найден.

[grizzly]

По сути в п.п.1--4 всё правильно, только записано коряво.

-- 19.04.2016, 00:34 --

gefest_md в сообщении #1116490 писал(а):

Если угол при точке $O$ прямой

Невозможно по построению:

gefest_md в сообщении #1116478 писал(а):

Перпендикуляр $OA$ и прямая $b$ образуют тупой и острый углы (рассматриваю этот случай).

[gefest_md]

grizzly в сообщении #1116501 писал(а):

По сути в п.п.1--4 всё правильно

Спасибо

grizzly в сообщении #1116501 писал(а):

Невозможно по построению

Я не строил, предположил, что угол не прямой, чтобы для этого случая (особенно) определить функцию $f$ и доказать существование общего перпендикуляра.

[gefest_md]

Теорему о существовании общего перпендикуляра можно доказать и по-другому. Сначала, не используя общий перпендикуляр, доказать утверждение: проекции всех точек одной из двух расходящихся прямых на другую заполняют на второй прямой лишь конечный отрезок. Затем можно доказать, что перпендикуляр восставленный из середины этого отрезка является общим.